题目内容
已知函数 .
.
(1)若函数 在区间
在区间 上有极值,求实数
上有极值,求实数 的取值范围;
的取值范围;
(2)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围;
的取值范围;
(3)当 ,
, 时,求证:
时,求证: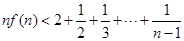 .
.
【答案】
(1)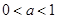
(2)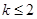
(3)根据数列的求和来放缩法得到不等式的证明关键是对于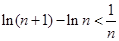 的运用。
的运用。
【解析】
试题分析:解:(1)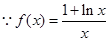 ,
,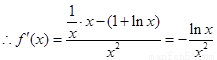
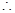 当
当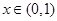 时,
时,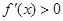 ;当
;当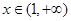 时,
时,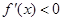 ;
;
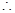 函数
函数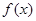 在区间(0,1)上为增函数;在区间
在区间(0,1)上为增函数;在区间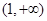 为减函数 3分
为减函数 3分
 当
当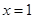 时,函数
时,函数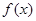 取得极大值,而函数
取得极大值,而函数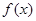 在区间
在区间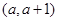 有极值.
有极值.
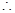
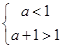 ,解得
,解得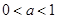 .
5分
.
5分
(2)由(1)得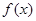 的极大值为
的极大值为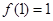 ,令
,令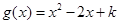 ,所以当
,所以当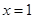 时,函数
时,函数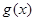 取得最小值
取得最小值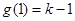 ,又因为方程
,又因为方程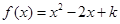 有实数解,那么
有实数解,那么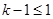 ,即
,即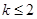 ,所以实数
,所以实数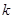 的取值范围是:
的取值范围是: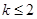 .
10分
.
10分
(另解: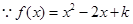 ,
,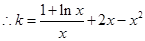 ,
,
令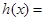
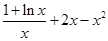 ,所以
,所以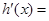
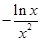
 ,当
,当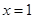 时,
时,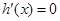
当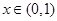 时,
时,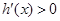 ;当
;当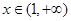 时,
时,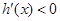
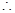 当
当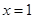 时,函数
时,函数 取得极大值为
取得极大值为
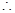 当方程
当方程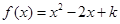 有实数解时,
有实数解时,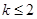 .)
.)
(3)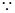 函数
函数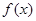 在区间
在区间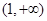 为减函数,而
为减函数,而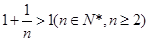 ,
,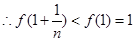
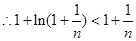 ,即
,即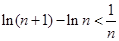
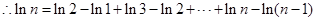
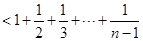 12分
12分
即 ,
,
而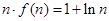 ,
,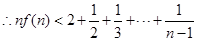 结论成立. 16分
结论成立. 16分
考点:导数的运用
点评:根据导数的符号判定函数的单调性,是解决该试题的关键,同时能结合函数与方程的思想求解方程的根,属于中档题。

练习册系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为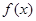 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素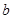 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程