题目内容
已知向量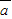 =(Asin
=(Asin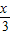 ,Acos
,Acos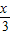 ),
),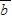 =(cos
=(cos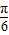 ,sin
,sin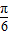 )函数f(x)=
)函数f(x)=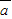 •
•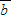 (A>0,x∈R),且f(2π)=2.
(A>0,x∈R),且f(2π)=2.(1)求函数y=f(x)的表达式;
(2)设α,β∈[0,
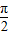 ],f(3α+π)=
],f(3α+π)=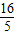 ,f(3β+
,f(3β+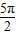 )=-
)=-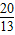 ,求cos(α+β)的值.
,求cos(α+β)的值.
【答案】分析:(1)利用向量的数量积和两角和的正弦公式即可得出;
(2)利用诱导公式、平方关系、两角和的余弦公式即可得出.
解答:解:(1)依题意得f(x)=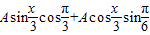 =A
=A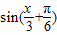 ,
,
∵f(2π)=2,∴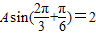 ,∴
,∴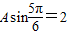 ,解得A=4.
,解得A=4.
∴f(x)=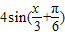 .
.
(2)由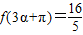 ,得
,得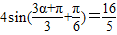 ,即
,即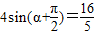 ,
,
∴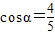
又∵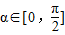 ,∴sinα=
,∴sinα=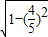 =
= ,
,
由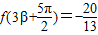 ,得
,得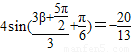 ,即
,即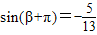 .
.
∴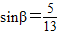 ,
,
又∵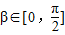 ,∴
,∴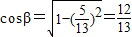 ,
,
∴cos(α+β)=cosαcosβ-sinαsinβ=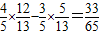 .
.
点评:熟练掌握向量的数量积运算和两角和的正弦公式、诱导公式、平方关系、两角和的余弦公式是解题的关键.
(2)利用诱导公式、平方关系、两角和的余弦公式即可得出.
解答:解:(1)依题意得f(x)=
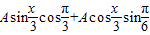 =A
=A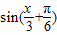 ,
,∵f(2π)=2,∴
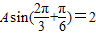 ,∴
,∴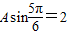 ,解得A=4.
,解得A=4.∴f(x)=
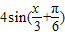 .
.(2)由
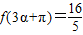 ,得
,得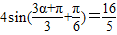 ,即
,即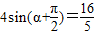 ,
,∴
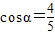
又∵
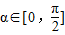 ,∴sinα=
,∴sinα=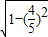 =
= ,
,由
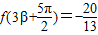 ,得
,得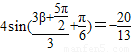 ,即
,即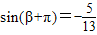 .
.∴
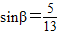 ,
,又∵
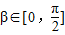 ,∴
,∴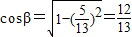 ,
,∴cos(α+β)=cosαcosβ-sinαsinβ=
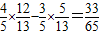 .
.点评:熟练掌握向量的数量积运算和两角和的正弦公式、诱导公式、平方关系、两角和的余弦公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,函数
,函数 .
.