题目内容
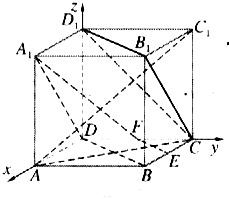 已知E,F分别是正方体ABCD-A1B1C1D1的棱BC和CD的中点,求:
已知E,F分别是正方体ABCD-A1B1C1D1的棱BC和CD的中点,求:(1)A1D与EF所成角的大小;
(2)A1F与平面B1EB所成角;
(3)二面角C-D1B1-B的大小.
分析:因为是正方休,又是空间角问题,所以易采用向量法,所以建立如图所示的空间直角坐标系D-xyz,(1)先求得相关点的坐标,再求得相关向量
=(-1,0,-1),
=(-
,-
,0),及其模|
|=
=
|
|=
=
再用向量的夹角公式求解.
(2)在正方体ABCD-A1B1C1D1中,因为AB⊥平面B1C1CB,所以
是平面B1EB的法向量,再用向量的夹角公式求解.
(3)先分别求得两个半平面的一个法向量,然后利用向量的夹角公式求解二面角.
| A1D |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| A1D |
| (-1)2+0+(-1)2 |
| 2 |
|
| EF |
(-
|
| ||
| 2 |
(2)在正方体ABCD-A1B1C1D1中,因为AB⊥平面B1C1CB,所以
| AB |
(3)先分别求得两个半平面的一个法向量,然后利用向量的夹角公式求解二面角.
解答:解:不妨设正方体的棱长为1,以
,
,
为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则各点的坐标为A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),C1(0,1,1),E(
,1,0),F(0,
,0)(1)因为
=(-1,0,-1),
=(-
,-
,0),
所以|
|=
=
|
|=
=
•
=
+0+0=
可知向量
与
的夹角为60°
因此A1D与EF所成角的大小为60°
(2)在正方体ABCD-A1B1C1D1中,因为AB⊥平面B1C1CB,所以
是平面B1EB的法向量
因为
=(1,1,0)-(1,0,0)=(0,1,0)
=(0,
,0)-(1,0,1)=(-1,
,-1)
所以|
|=1,|
|=
,
•
=
,
由cos<
,
>=
,
所以可得向量之间的夹角约为:19.47°
(3)因为AC1⊥平面B1D1C,所以
是平面B1D1C的法向量,因为
=(-1,1,1),
=(-1,1,0),|
|=
,|
|=
,
•
=2
所以cos<
,
>=
,所以可得两向量的夹角为35.26°
根据二面角夹角相等或互补可知,二面角约为:35.26°
| DA |
| DC |
| DD1 |
| 1 |
| 2 |
| 1 |
| 2 |
| A1D |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
所以|
| A1D |
| (-1)2+0+(-1)2 |
| 2 |
|
| EF |
(-
|
| ||
| 2 |
| A1D |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
可知向量
| A1D |
| EF |
因此A1D与EF所成角的大小为60°
(2)在正方体ABCD-A1B1C1D1中,因为AB⊥平面B1C1CB,所以
| AB |
因为
| AB |
| A1F |
| 1 |
| 2 |
| 1 |
| 2 |
所以|
| AB |
| A1F |
| 3 |
| 2 |
| A1F |
| AB |
| 1 |
| 2 |
由cos<
| A1F |
| AB |
| 1 |
| 3 |
所以可得向量之间的夹角约为:19.47°
(3)因为AC1⊥平面B1D1C,所以
| AC1 |
| AC1 |
| AC |
| AC1 |
| 3 |
| AC |
| 2 |
| AC1 |
| AC |
所以cos<
| AC1 |
| AC |
| ||
| 3 |
根据二面角夹角相等或互补可知,二面角约为:35.26°
点评:本题主要考查向量法在求空间角中的应用,在研究空间角时,要首选向量法,方便灵活,是常考类型,属中档题.

练习册系列答案
相关题目
 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.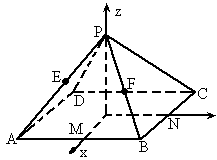
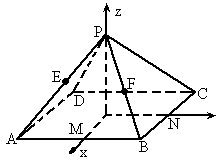
 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.