题目内容
已知函数f(x)=x2ln(ax)(a>0)
(1)若f′(x)≤x2对任意的x>0恒成立,求实数a的取值范围;
(2)当a=1时,设函数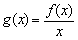 ,若x1,x2∈(
,若x1,x2∈( ,1),x1+x2<1,求证:x1x2<(x1+x2)4。
,1),x1+x2<1,求证:x1x2<(x1+x2)4。
解:(1)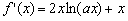
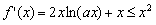
即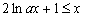 在
在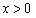 上恒成立
上恒成立
设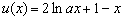
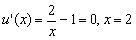
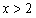 时,单调减
时,单调减
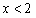 时,单调增
时,单调增
所以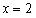 时,
时,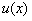 有最大值
有最大值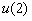
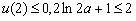
所以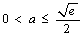 。
。
(2)当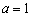 时,
时,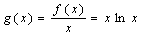
g′(x)=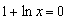
∴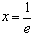
所以在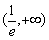 上
上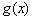 是增函数
是增函数
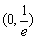 上是减函数
上是减函数
因为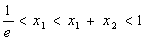
所以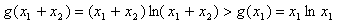
即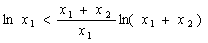
同理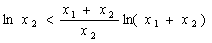
所以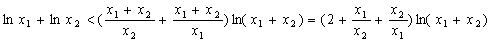
又因为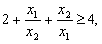
当且仅当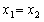 时,取等号
时,取等号
又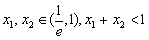
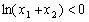
所以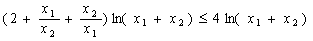
所以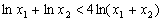
所以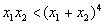 。
。
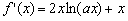
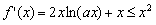
即
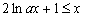 在
在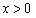 上恒成立
上恒成立设
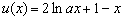
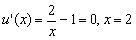
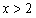 时,单调减
时,单调减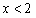 时,单调增
时,单调增所以
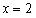 时,
时,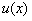 有最大值
有最大值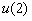
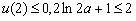
所以
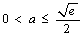 。
。(2)当
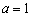 时,
时,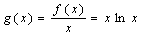
g′(x)=
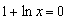
∴
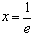
所以在
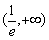 上
上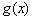 是增函数
是增函数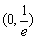 上是减函数
上是减函数因为
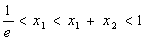
所以
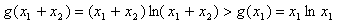
即
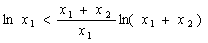
同理
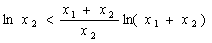
所以
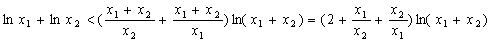
又因为
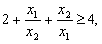
当且仅当
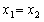 时,取等号
时,取等号又
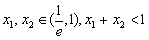
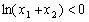
所以
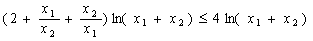
所以
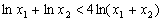
所以
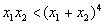 。
。
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|