题目内容
已知函数f(x)=x3+bx2+cx在x=1处的切线方程为6x-2y-1=0,f′(x)为f(x)的导函数,g(x)=a•ex(a,b,c∈R).
(1)求b,c的值;
(2)若存在x0∈(0,2],使g(x0)=f′(x0)成立,求a的范围.
解:(1)∵f′(x)=3x2+2bx+c,
∴f(x)在x=1处的切线方程为y-(1+b+c)=(3+2b+c)(x-1),
即y=(3+2b+c)x-2-b,
∴ ,即
,即 ,
,
∴ .
.
(2)若存在x0∈(0,2]使 成立,
成立,
即方程g(x)=f′(x)在(0,2]上有解,
∴a•ex=3x2-3x+3,
∴ ,
,
令 ,
,
∴
=
=- ,
,
令h′(x)=0,得x1=1,x2=2,列表讨论:
∴h(x)有极小值h(1)=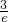 ,h(x)有极大值h(2)=
,h(x)有极大值h(2)= ,
,
且当x→0时,h(x)→3> ,
,
∴a的取值范围是 .
.
分析:(1)由f′(x)=3x2+2bx+c,知f(x)在x=1处的切线方程为y=(3+2b+c)x-2-b,故 ,由此能求出f(x).
,由此能求出f(x).
(2)若存在x0∈(0,2]使 成立,即方程g(x)=f′(x)在(0,2]上有解,故
成立,即方程g(x)=f′(x)在(0,2]上有解,故 ,令
,令 ,则
,则 =-
=- ,由此能求出a的取值范围.
,由此能求出a的取值范围.
点评:本题考查实数值和实数取值范围的求法,具体涉及到导数的应用、函数极值的求法和应用、切线方程的求法和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
∴f(x)在x=1处的切线方程为y-(1+b+c)=(3+2b+c)(x-1),
即y=(3+2b+c)x-2-b,
∴
 ,即
,即 ,
,∴
 .
.(2)若存在x0∈(0,2]使
 成立,
成立,即方程g(x)=f′(x)在(0,2]上有解,
∴a•ex=3x2-3x+3,
∴
 ,
,令
 ,
,∴

=

=-
 ,
,令h′(x)=0,得x1=1,x2=2,列表讨论:
| x | (0,1) | 1 | (1,2) | 2 |
| h′(x) | - | 0 | + | 0 |
| h(x) | ↓ | 极小值 | ↑ | 极大值 |
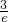 ,h(x)有极大值h(2)=
,h(x)有极大值h(2)= ,
,且当x→0时,h(x)→3>
 ,
,∴a的取值范围是
 .
.分析:(1)由f′(x)=3x2+2bx+c,知f(x)在x=1处的切线方程为y=(3+2b+c)x-2-b,故
 ,由此能求出f(x).
,由此能求出f(x).(2)若存在x0∈(0,2]使
 成立,即方程g(x)=f′(x)在(0,2]上有解,故
成立,即方程g(x)=f′(x)在(0,2]上有解,故 ,令
,令 ,则
,则 =-
=- ,由此能求出a的取值范围.
,由此能求出a的取值范围.点评:本题考查实数值和实数取值范围的求法,具体涉及到导数的应用、函数极值的求法和应用、切线方程的求法和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|