题目内容
5.己知PE、PF是⊙O的切线,A、B是一组对径点,PB交⊙O于另一点C,直线AF、BE交于D点.求证:∠PCD=∠PCE.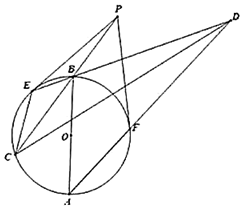
分析 连接AE,OE,OF,PD.可得∠AEB=∠OEP=∠OFP=90°,OE=OB=OA=OF,∠OEF=∠OFE=$\frac{1}{2}$∠EPF,∠PEB=∠PCE,∠OEB=∠OBE.可得:点D在以P为圆心,PE的长为半径的圆上.进而证明E,C,D,P四点共圆,即可得出结论.
解答 证明:连接AE,OE,OF,PD.可得∠AEB=∠OEP=∠OFP=90°,OE=OB=OA=OF,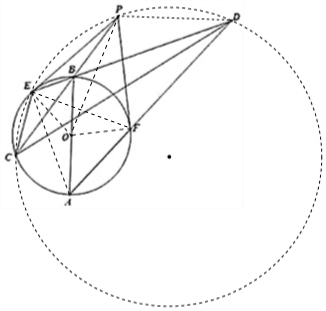
∠OEF=∠OFE=$\frac{1}{2}$∠EPF,∠PEB=∠PCE,
∠OEB=∠OBE.
∵∠EDA=∠EBA-∠BAD=∠BEO-∠BEF=∠OEF=$\frac{1}{2}∠EPF$,PE=PF.
∴点D在以P为圆心,PE的长为半径的圆上.
∴PE=PD,∴∠PED=∠PDE,∠ECP=∠PDE,
∴E,C,D,P四点共圆,
∴∠PED=∠PCD.
∴∠PCD=∠PCE.
点评 本题考查了圆的性质、圆的切线的性质、四点共圆,本题条件比较多,考查了较强的推理能力与计算能力,属于难题.

练习册系列答案
相关题目
6.双曲线 $\frac{x^2}{{1+{k^2}}}-\frac{y^2}{{8-{k^2}}}=1$(k为常数)的焦点坐标是( )
| A. | (0,±3) | B. | (±3,0) | C. | (±1,0) | D. | (0,±1) |
13.设Sn为等差数列{an}的前n项和,a1=-2,S3=0,则{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中不正确的序号有( )
①若α⊥β,α∩β=m,且n⊥m,则n⊥α或n⊥β
②若m不垂直于α,则m不可能垂直于α内的无数条直线
③若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β
④若α⊥β,m∥n,n⊥β,则m∥α
①若α⊥β,α∩β=m,且n⊥m,则n⊥α或n⊥β
②若m不垂直于α,则m不可能垂直于α内的无数条直线
③若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β
④若α⊥β,m∥n,n⊥β,则m∥α
| A. | ①②③④ | B. | ③ | C. | ①④ | D. | ①②④ |
17.已知两条不同直线a,b及平面α,则下列命题中真命题是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥b,b∥α,则a∥α | C. | 若a⊥α,b⊥α,则a∥b | D. | 若a⊥α,b⊥a,则b⊥α |
14.设$a={({\frac{1}{2}})^{\frac{1}{2}}},b={({\frac{1}{2}})^{\frac{1}{3}}},c={log_{\frac{1}{2}}}2$,则( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
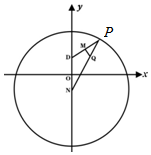 如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.
如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.