题目内容
【题目】给出下列说法:
①方程![]() 表示一个圆;
表示一个圆;
②若![]() ,则方程
,则方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;
轴上的椭圆;
③已知点![]() ,若
,若![]() ,则动点
,则动点![]() 的轨迹是双曲线的右支;
的轨迹是双曲线的右支;
④以过抛物线焦点的弦为直径的圆与该抛物线的准线相切,
其中正确说法的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据题意,依次分析题目中的四个命题,综合即可得答案.
根据题意,
对于①,方程![]() 变形为
变形为![]() ,不是圆的方程,
,不是圆的方程,
故①错误;
对于②,方程![]() 变形为
变形为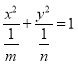 ,若
,若![]() ,则有
,则有![]() ,则方程表示焦点在
,则方程表示焦点在![]() 轴上的椭圆,故②错误;
轴上的椭圆,故②错误;
对于③,点![]() ,则
,则![]() ,若
,若![]() ,则动点
,则动点![]() 的轨迹是一条射线(以
的轨迹是一条射线(以![]() 为端点向右的射线),故③错误;
为端点向右的射线),故③错误;
对于④,设抛物线方程为![]() ,焦点坐标为
,焦点坐标为![]() ,准线方程为
,准线方程为![]() ,
,
过焦点的弦为![]() ,过端点
,过端点![]() ,
,![]() 分别做准线的垂线,垂足为
分别做准线的垂线,垂足为![]() ,
,![]() ,由抛物线的定义知,
,由抛物线的定义知,
![]() ,
,![]() ,则
,则![]() ,
,
由梯形的中位线知,![]() ,即以过抛物线焦点的弦为直径的圆与该抛物线的准线相切,故④正确.
,即以过抛物线焦点的弦为直径的圆与该抛物线的准线相切,故④正确.
综上,正确说法的个数为![]() 个.
个.
故选:B.

练习册系列答案
相关题目



