题目内容
已知数列{an}的首项为1,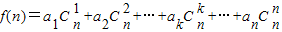 (n∈N+).
(n∈N+).(1)若{an}为常数列,求f(4)的值;
(2)若{an}为公比为2的等比数列,求f(n)的解析式;
(3)数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立.若能,求出数列{an}的通项公式;若不能,试说明理由.
【答案】分析:(1)根据{an}为常数列,且首项为1,可得它的通项公式.
(2)若{an}为公比为2的等比数列,则an=2n-1,(n∈N+),用二项式定理以及倒序相加法求得f(n)的解析式.
(3)假设数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立,设公差为d,用倒序相加法求得f(n)的解析式为 1+(n-1)2n ,可得(d-2)+[2+(n-2)d]•2n-1=0 n∈N+都成立,可得d=2,从而求得数列{an}的通项公式.
解答:解:(1)∵{an}为常数列,且首项为1,故有an=1,
∴f(4)=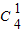 +
+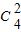 +
+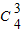 +
+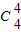 =15.
=15.
(2)若{an}为公比为2的等比数列,则an=2n-1,(n∈N+).
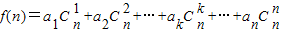 =
=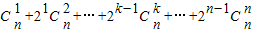 ,
,
故1+2f(n)=1+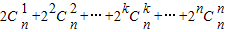 =(1+2)n=3n,
=(1+2)n=3n,
∴f(n)=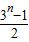 .
.
(3)假设数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立.
设公差为d,则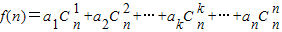 ①,
①,
且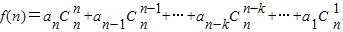 ②,
②,
把①、②相加可得 2f(n)=2an+(a1+an-1)(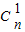 +
+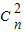 +
+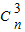 +…+
+…+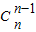 )
)
∴f(n)=an+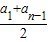 (
(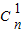 +
+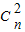 +
+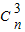 +…+
+…+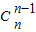 )
)
=an+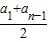 (2n-2)=1+(n-1)d+[2+(n-2)d](2n-1-1).
(2n-2)=1+(n-1)d+[2+(n-2)d](2n-1-1).
∴f(n)-1=(d-2)+[2+(n-2)d]]•2n-1=(n-1)2n 恒成立.
即 (d-2)+(d-2)•[n+2]•2n-1=0 n∈N+都成立,∴d=2,
故存在数列{an}使得f(n)-1=(n-1)2n对一切n∈N+都成立,且通项公式为an=2n-1.(其它方法相应给分)
点评:本题主要考查二项式定理的应用,等差关系的确定,等差数列的通项公式,属于中档题.
(2)若{an}为公比为2的等比数列,则an=2n-1,(n∈N+),用二项式定理以及倒序相加法求得f(n)的解析式.
(3)假设数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立,设公差为d,用倒序相加法求得f(n)的解析式为 1+(n-1)2n ,可得(d-2)+[2+(n-2)d]•2n-1=0 n∈N+都成立,可得d=2,从而求得数列{an}的通项公式.
解答:解:(1)∵{an}为常数列,且首项为1,故有an=1,
∴f(4)=
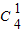 +
+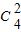 +
+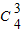 +
+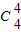 =15.
=15.(2)若{an}为公比为2的等比数列,则an=2n-1,(n∈N+).
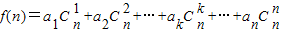 =
=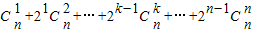 ,
,故1+2f(n)=1+
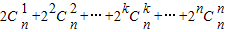 =(1+2)n=3n,
=(1+2)n=3n,∴f(n)=
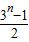 .
.(3)假设数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立.
设公差为d,则
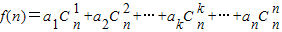 ①,
①,且
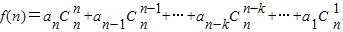 ②,
②,把①、②相加可得 2f(n)=2an+(a1+an-1)(
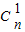 +
+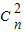 +
+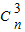 +…+
+…+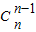 )
) ∴f(n)=an+
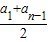 (
(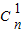 +
+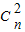 +
+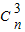 +…+
+…+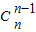 )
) =an+
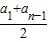 (2n-2)=1+(n-1)d+[2+(n-2)d](2n-1-1).
(2n-2)=1+(n-1)d+[2+(n-2)d](2n-1-1).∴f(n)-1=(d-2)+[2+(n-2)d]]•2n-1=(n-1)2n 恒成立.
即 (d-2)+(d-2)•[n+2]•2n-1=0 n∈N+都成立,∴d=2,
故存在数列{an}使得f(n)-1=(n-1)2n对一切n∈N+都成立,且通项公式为an=2n-1.(其它方法相应给分)
点评:本题主要考查二项式定理的应用,等差关系的确定,等差数列的通项公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目