题目内容
已知θ为第二象限角,且sinθ+cosθ= ,那么tanθ=
,那么tanθ=
- A.-
 或-
或-
- B.-

- C.-

- D.-

B
分析:通过θ为第二象限角,且sinθ+cosθ= ,利用平方关系,确定sinx-cosx>0,求出sinx-cosx的值,求解sinx,cosx,得到tanx的值.
,利用平方关系,确定sinx-cosx>0,求出sinx-cosx的值,求解sinx,cosx,得到tanx的值.
解答:因为sinx+cosx= ,而sin2x+cos2x=1
,而sin2x+cos2x=1
即(sinx+cosx)2-2sinxcosx=1,所以 -2sinxcosx=1
-2sinxcosx=1
所以2sinxcosx=-
又因为sin2x+cos2x=(sinx-cosx)2+2sinxcosx=1
所以(sinx-cosx)2- =1,所以(sinx-cosx)2=
=1,所以(sinx-cosx)2=
又因为0<x<180°,所以sinx>0,而2sinxcosx=- <0,所以cosx<0
<0,所以cosx<0
所以sinx-cosx>0,所以sinx-cosx=
和sinx+cosx= 相加得:sinx=
相加得:sinx= ,所以cosx=-
,所以cosx=-
所以tanx=-
故选B
点评:本题是基础题,解题方法规范、典型;考查利用诱导公式化简求值,本题是选择题,判定象限三角函数的符号,以及θ为第二象限角,且sinθ+cosθ= ,容易知道sinx=
,容易知道sinx= ,cosx=-
,cosx=- ,求出tanx=-
,求出tanx=- ,此外还有
,此外还有 、
、 一组数据关系,都是满足勾股定理.灵活记忆,在解选择题,填空题是省时省力.
一组数据关系,都是满足勾股定理.灵活记忆,在解选择题,填空题是省时省力.
分析:通过θ为第二象限角,且sinθ+cosθ=
 ,利用平方关系,确定sinx-cosx>0,求出sinx-cosx的值,求解sinx,cosx,得到tanx的值.
,利用平方关系,确定sinx-cosx>0,求出sinx-cosx的值,求解sinx,cosx,得到tanx的值.解答:因为sinx+cosx=
 ,而sin2x+cos2x=1
,而sin2x+cos2x=1 即(sinx+cosx)2-2sinxcosx=1,所以
 -2sinxcosx=1
-2sinxcosx=1 所以2sinxcosx=-

又因为sin2x+cos2x=(sinx-cosx)2+2sinxcosx=1
所以(sinx-cosx)2-
 =1,所以(sinx-cosx)2=
=1,所以(sinx-cosx)2=
又因为0<x<180°,所以sinx>0,而2sinxcosx=-
 <0,所以cosx<0
<0,所以cosx<0 所以sinx-cosx>0,所以sinx-cosx=

和sinx+cosx=
 相加得:sinx=
相加得:sinx= ,所以cosx=-
,所以cosx=-
所以tanx=-

故选B
点评:本题是基础题,解题方法规范、典型;考查利用诱导公式化简求值,本题是选择题,判定象限三角函数的符号,以及θ为第二象限角,且sinθ+cosθ=
 ,容易知道sinx=
,容易知道sinx= ,cosx=-
,cosx=- ,求出tanx=-
,求出tanx=- ,此外还有
,此外还有 、
、 一组数据关系,都是满足勾股定理.灵活记忆,在解选择题,填空题是省时省力.
一组数据关系,都是满足勾股定理.灵活记忆,在解选择题,填空题是省时省力. 
练习册系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求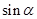 和
和 及
及 的值.
的值.