题目内容
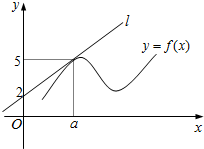
如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）= ．
【答案】分析：先利用图象得出切线方程，然后利用切线斜率k与f′（4）的关系确定f′（4）的值．
解答：解：由图象可知，切线过点（4，5）和（0，3），
不防设切线方程为y=kx+b，将点（4，5）和（0，3）代入切线方程得
，解得
，即切线方程为
．
又因为k=f'（4），所以
．
故答案为：
．
点评：本题考查了导数的几何意义以及直线方程的求法，对于相应的运算公式要求熟练掌握．
解答：解：由图象可知，切线过点（4，5）和（0，3），
不防设切线方程为y=kx+b，将点（4，5）和（0，3）代入切线方程得
，解得，即切线方程为．又因为k=f'（4），所以
．故答案为：
．点评：本题考查了导数的几何意义以及直线方程的求法，对于相应的运算公式要求熟练掌握．
练习册系列答案
相关题目
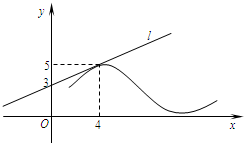如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）=
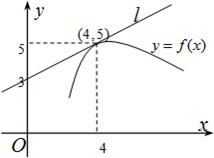如图，直线l是曲线y=f（x）在（4，5）处的切线，则f′（4）=