题目内容
(14分) 已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、
第十四项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=![]() (n∈N*),Sn=b1+b2+…+bn,求Sn ;
(n∈N*),Sn=b1+b2+…+bn,求Sn ;
(Ⅲ)对于(Ⅱ)中的Sn ,是否存在实数t,使得对任意的n均有:![]()
成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
(14分) 解:(Ⅰ)由题意得(a1+d)(a1+13d)=(a1+4d)2,
整理得2a1d=d2.
∵a1=1,解得(d=0舍),d=2.
∴an=2n-1(n∈N*).
(Ⅱ)bn=![]() =
=![]() =
=![]() (
(![]() -
-![]() ),
),
∴Sn=b1+b2+…+bn=![]() [(1-
[(1-![]() )+(
)+(![]() -
-![]() )+…+(
)+…+(![]() -
-![]() )]
)]
=![]() (1-
(1-![]() )=
)=![]() .
.
(Ⅲ)假设存在整数t满足![]() 总成立.
总成立.
得![]() ,而
,而 ,即
,即![]() ,
,
∴![]() 适合
适合

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
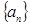 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值. 中,
中, ,且
,且 是
是 和
和 的等差中项.
的等差中项. 满足
满足 ,求
,求 项和
项和 .
. 的图象是曲线C,点
的图象是曲线C,点 是曲线C上的一系列点,
是曲线C上的一系列点, 处的切线与y轴交于点
处的切线与y轴交于点 。若数列
。若数列 是公差为2的等差
是公差为2的等差
 与数列
与数列 表示
表示 的面积,求数列
的面积,求数列 的前项n和
的前项n和