Question

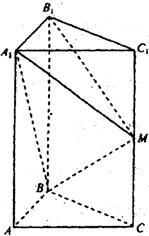如图，在直三棱柱ABC-A₁B₁C₁中，∠ABC=90°，AC=2AB=4，AA₁=4

3

，M为CC₁的中点．
（I）求证：BM⊥平面A₁B₁M；
（II）求平面A₁BM与平面ABC所成锐二面角的大小；
（III）求点C到平面A₁BM的距离．

Answer 1

分析：（I）因为ABC-A₁B₁C₁是直三棱柱，所以平面A₁B₁C₁⊥平面B₁BCC₁，由A₁B₁⊥B₁C，知A₁B₁⊥平面B₁BCC₁，所以BM⊥A₁B₁，由此能够证明BM⊥平面A₁B₁M．
（II）设A₁M∩AC=E，连接BE，作CF⊥BE，垂足为F，连接MF，则BE⊥MF．于是∠MFC为所求二面角的平面角．由此能求出平面A₁BM与平面ABC所成锐二面角的大小．
（III）作CH⊥FM，垂足为H，由BF⊥平面CFM，知平面A₁BM⊥平面CFM，所以CH⊥平面A₁BM，由此能求出点C到平面A₁BM的距离．

解答：解：（I）因为ABC-A₁B₁C₁是直三棱柱，
所以平面A₁B₁C₁⊥平面B₁BCC₁，
∵A₁B₁⊥B₁C，∴A₁B₁⊥平面B₁BCC₁，∴BM⊥A₁B₁，
∵AC=2AB=4，∠ABC=90°∴角BAC=60°，∴BC=2

3

，
由已知，CM=C₁M=2

3

，∴∠BMC=∠B₁MC₁=45°，∠BMB₁=90°，
即BM⊥B₁M，又A₁B₁∩B₁M=B₁，
∴BM⊥平面A₁B₁M，…（4分）
（II）设A₁M∩AC=E，连接BE，作CF⊥BE，垂足为F，连接MF，则BE⊥MF．
于是∠MFC为所求二面角的平面角．  …（5分）
由M是CC₁中点，知CE=AC=4，在△BCE中，∠BCE=150°，
BE=

BC2+CE2-2BC•CE•cos150°

=2

13

．
∵

1

2

BE•CF=

1

2

BC•CE•sin150°，
∴

1

2

×2

13

×CF=

1

2

×2

3

×4×

1

2

，
∴CF=

2 3

13

，
tan∠MFC=

CM

CF

=

13

，…（6分）
所以平面A₁BM与平面ABC所成锐二面角的大小为arctan

13

．…（8分）
（III）作CH⊥FM，垂足为H，
由（II）的解答，知BF⊥平面CFM，
则平面A₁BM⊥平面CFM，所以CH⊥平面A₁BM，CH即所求
∵tan∠MFC=

13

，
∴sin∠MFC=

13

14

，
∴CH=CFsin∠MFC=

42

7

为所求．
即点C到平面A₁BM的距离是

42

7

．…（12分）

点评：本题考查二面角的求法和求点到平面的距离，考查运算求解能力，推理论证能力；考查化归与转化思想．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．