Question

已知α为锐角，且．
（1）设=（x，1），=（2tan2α，sin（2α+）），若，求x的值；
（2）在△ABC中，若∠A=2α，，BC=2，求△ABC的面积．

Answer 1

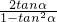解：（1）∵，tan2α===1．
又∵α为锐角，∴2α=，α=，=（2，1）． 
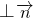∵，∴=0，即 2x+1=0，x=-．

（2）由（1）得∠A=，而，根据正弦定理得，
求得，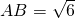
∴，
从而求得△ABC的面积．

分析：（1）利用二倍角的正切公式求得tan2α 的值，可得2α=，再由=0求得x的值．
（2）由（1）得∠A=，而，根据正弦定理求得AB的值，可得sinB的值，从而求得△ABC的面积．
点评：本题主要考查三角函数的恒等变换，向量的数量积公式的应用，两个向量垂直的性质，属于中档题．