题目内容
如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D、E、F分别是BC、CA、AA1的中点,AA1=AB=4.

(Ⅰ)求证:EF∥平面AB1D;
(Ⅱ)求三棱锥B1-AA1D的体积.
(Ⅰ)连接A1B交AB1于O,连接OD,在△BA1C中,O为BA1中点,D为BC中点,∴OD∥A1C.
又∵E、F分别为CA、AA1的中点,∴EF∥A1C,因此EF∥OD. 
∵OD⊂平面AB1D,EF⊄平面AB1D,
∴EF∥平面AB1D.
(Ⅱ)由(Ⅰ)可知,OD∥A1C,∵OD⊂平面AB1D,A1C⊄平面AB1D,∴A1C∥平面AB1D,∴点A1到平面AB1D的距离等于点C到平面AB1D的距离,
∵S△ADC=S△ABC=2 ,∴
,∴ =
= ×4×2
×4×2 .
.

练习册系列答案
相关题目
 的
的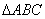 内任投一点
内任投一点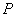 ,则
,则 的面积大于
的面积大于 的概率为________.
的概率为________.  满足约束条件
满足约束条件 ,则
,则 的最小值为 .
的最小值为 . 的图象向左平移个单位,再向上平移个单位,所得图象的函数解析式是
的图象向左平移个单位,再向上平移个单位,所得图象的函数解析式是 B.
B.
 D.
D.
 是定义在R上的偶函数,当
是定义在R上的偶函数,当 0时,
0时, ,如果函数
,如果函数 (m∈R) 恰有4个零点,则m的取值范围是____.
(m∈R) 恰有4个零点,则m的取值范围是____. =(1,2),
=(1,2), =(x,-4),若
=(x,-4),若 ( )
( )
 中,
中, ,
, ,则
,则 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( ) .
.
 .
.
 .
.
 .
.
 C.
C.  <a<5 D.
<a<5 D.  满足
满足 为虚数单位),则
为虚数单位),则 ( )
( ) B.
B.  C.
C.  D.
D. 