题目内容
已知函数![]()
(1)当![]() 且
且![]() 时,①求
时,①求![]() 的值;②求
的值;②求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的定义域、值域都是
的定义域、值域都是![]() ,若存在,则求出
,若存在,则求出![]() 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
解:(1) ∵
∴![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上是增函数.
上是增函数.
①由![]() ,且
,且![]() ,可得
,可得![]() 且
且![]() .所以
.所以![]() .
.
②由①知![]() ∴
∴![]()
![]()
∵![]() 且
且![]() ∴
∴![]()
∴![]()
![]()
(2)不存在满足条件的实数![]() .
.
若存在满足条件的实数![]() , 则
, 则![]()
① 当![]() 时,
时,![]() 在
在![]() 上为减函数.
上为减函数.
故![]() 即
即 解得
解得![]()
故此时不存在适合条件的实数![]() .
.
② 当![]() 时,
时,![]() 在
在![]() 上是增函数.
上是增函数.
故![]() 即
即
此时![]() 是方程
是方程![]() 的根,此方程无实根.
的根,此方程无实根.
故此时不存在适合条件的实数![]() .
.
当![]() 时,由于
时,由于![]() ,而
,而![]() ,
,
故此时不存在适合条件的实数![]() .
.
综上可知,不存在适合条件的实数![]() .
.

练习册系列答案
相关题目
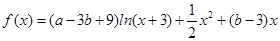 .
.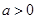 且
且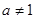 ,
,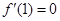 时,试用含
时,试用含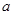 的式子表示
的式子表示 ,并讨论
,并讨论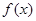 的单调区间;
的单调区间;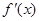 有零点,
有零点,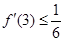 ,且对函数定义域内一切满足
,且对函数定义域内一切满足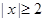 的实数
的实数 有
有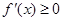 .
. 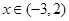 时,求函数
时,求函数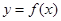 的图象与函数
的图象与函数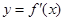 的图象的交点坐标
的图象的交点坐标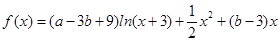 .
.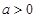 且
且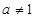 ,
,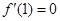 时,试用含
时,试用含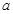 的式子表示
的式子表示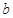 ,并讨论
,并讨论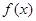 的单调区间;
的单调区间;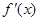 有零点,
有零点,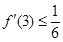 ,且对函数定义域内一切满足
,且对函数定义域内一切满足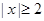 的实数
的实数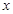 有
有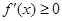 .
. 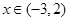 时,求函数
时,求函数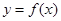 的图象与函数
的图象与函数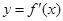 的图象的交点坐标.
的图象的交点坐标. 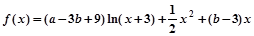 .
. 且
且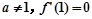 ,时,试用含
,时,试用含 的式子表示
的式子表示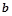 ,并讨论
,并讨论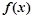 的单调区间;
的单调区间;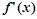 有零点,
有零点, ,且对函数定义域内一切满足|x|≥2的实数x有
,且对函数定义域内一切满足|x|≥2的实数x有 时,求函数
时,求函数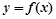 的图象与函数
的图象与函数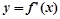 的图象的交点坐标.
的图象的交点坐标.