题目内容
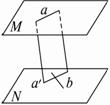
已知a、b是异面直线，平面M过a且平行于b，平面N过b且平行于a，求证：平面M∥平面N.
解析:欲证面面平行，需证线面平行，即在一个平面内找到两条相交直线平行于另一个平面. 证明:如图，过a作平面使它交平面N于a′, ∵a∥N, ∴a∥a′. 又a ∴a′∥平面M. ∵a和b是异面直线， ∴a′和b相交，由a′∥平面M，b∥平面M，得平面M∥平面N. 点评:要证面面平行，只要证线面平行，而要证线面平行，只要证线线平行.在立体几何中，往往通过线线、线面、面面间的位置关系的转化使问题得到解决.熟练掌握这种转化的思想方法，就能找到解题的突破口.本题也可用反证法.
平面M，a′
M,
练习册系列答案
课课练与单元测试系列答案
世纪金榜小博士单元期末一卷通系列答案
单元测试AB卷台海出版社系列答案
黄冈新思维培优考王单元加期末卷系列答案
名校名师夺冠金卷系列答案
小学英语课时练系列答案
培优新帮手系列答案
课堂作业广西教育出版社系列答案
相关题目
