题目内容
3.求下列函数的值域(1)y=log2(x2-4x+6);
(2)y=log2$\frac{1}{-{x}^{2}+2x+2}$;
(3)y=log2(x2-4x-5).
分析 (1)配方得x2-4x+6=(x-2)2+2,从而求函数的值域;
(2)化简$\frac{1}{-{x}^{2}+2x+2}$=$\frac{1}{-(x-1)^{2}+3}$,从而可得$\frac{1}{-(x-1)^{2}+3}$∈[$\frac{1}{3}$,+∞),从而解得;
(3)配方得x2-4x-5=(x-2)2-9,从而求函数的值域.
解答 解:(1)∵x2-4x+6=(x-2)2+2≥2,
∴y=log2(x2-4x+6)≥log22=1;
∴函数的值域为[1,+∞);
(2)∵$\frac{1}{-{x}^{2}+2x+2}$=$\frac{1}{-(x-1)^{2}+3}$,
∴$\frac{1}{-(x-1)^{2}+3}$∈[$\frac{1}{3}$,+∞),
∴y=log2$\frac{1}{-{x}^{2}+2x+2}$≥log2$\frac{1}{3}$=-log23;
∴函数的值域为[-log23,+∞);
(3)∵x2-4x-5=(x-2)2-9,
∴(x-2)2-9∈(0,+∞),
∴y=log2(x2-4x-5)∈R,
∴函数的值域为R.
点评 本题考查了函数的值域的求法及应用.

练习册系列答案
相关题目
13.下列语句是命题的是( )
| A. | 今天天气真好啊! | B. | 你怎么又没交作业? | ||
| C. | x>2 | D. | ?x∈R,x>2 |
14.设a=($\frac{2}{5}$)${\;}^{\frac{2}{5}}$,b=($\frac{2}{5}$)${\;}^{\frac{3}{5}}$,c=log${\;}_{\frac{1}{4}}$3,则a,b,c的大小关系是( )
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | c>b>a |
18.给出下列函数:①y=x3+1②y=lg$\frac{1+x}{1-x}$③y=x$+\frac{2}{x}$④y=ln($\sqrt{{x}^{2}+1}-x$),其中奇函数的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.函数f(x)=Asin(wx+φ)(A>0,w>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{3π}{2}$)的值是( )
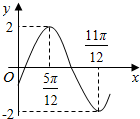

| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |