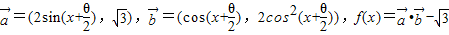题目内容
已知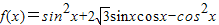
（1）求f（x）的最大值及取最大值时x的集合．
（2）求f（x）的增区间．
【答案】分析：（1）先利用二倍角公式将函数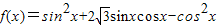
化为
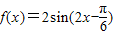，结合正弦函数的图象和性质，当
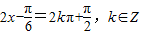时函数取最大值，解不等式即可．
（2）将内层函数作为整体，放到正弦曲线的增区间上，即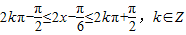
，解不等式即可得此复合函数的单调增区间．
解答：解：由已知：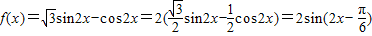
，
（1）当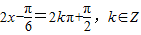
，
即：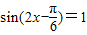
时，f（x）取最大值2．
此时x的集合为：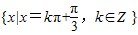
（2）∵
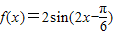
由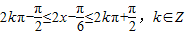
，
得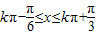
，k∈Z
∴f（x）的增区间为：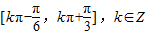
点评：本题考查了二倍角公式，三角变换方法，正弦曲线的性质，求复合函数单调区间的方法属于三角函数的性质的综合运用．
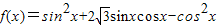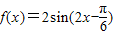化为，结合正弦函数的图象和性质，当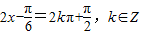时函数取最大值，解不等式即可．（2）将内层函数作为整体，放到正弦曲线的增区间上，即
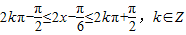，解不等式即可得此复合函数的单调增区间．解答：解：由已知：
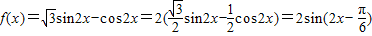，（1）当
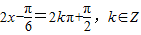，即：
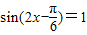时，f（x）取最大值2．此时x的集合为：
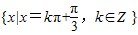
（2）∵
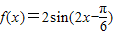
由
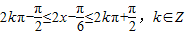，得
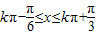，k∈Z∴f（x）的增区间为：
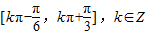
点评：本题考查了二倍角公式，三角变换方法，正弦曲线的性质，求复合函数单调区间的方法属于三角函数的性质的综合运用．
练习册系列答案
相关题目
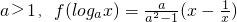
时，f（x）的最小值为2，求f（x）≥2成立的x的取值集合．
的值．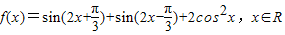
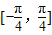上没有零点，求m的取值范围．
