题目内容
已知函数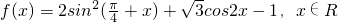 .
.
(1)求函数f(x)的最小正周期和单调增区间;
(2)函数f(x)的图象由函数y=sinx的图象经过怎样的变换得到?(写出变换过程)
(3)在△ABC中,若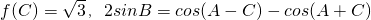 ,求tanA的值.
,求tanA的值.
解:(1)∵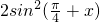 =
=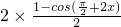 =1-
=1-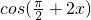 =1+sin2x,
=1+sin2x,
∴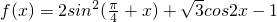 =sin2x+
=sin2x+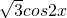 =
=
所以f(x)的最小正周期T= =π,
=π,
由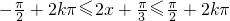 ,解得
,解得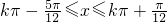
∴函数f(x)的单增区间为[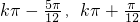 ],k∈Z
],k∈Z
(2)函数f(x)的图象可由函数y=sinx的图象先向左平移 个单位,
个单位,
然后将图象上的点纵坐标不变,横坐标缩短为原来的 ,最后将图象上的点横坐标不变,纵坐标伸长为原来的2倍而得.
,最后将图象上的点横坐标不变,纵坐标伸长为原来的2倍而得.
(3)由(1)得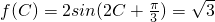 ,所以
,所以
∵0<C<π,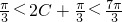 ,
,
∴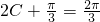 ,可得
,可得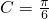 ,
,
∵在△ABC中,π-B=A+C,得sinB=sin(A+C)
∴2sinB=cos(A-C)-cos(A+C)可化为:2sin(A+C)=cos(A-C)-cos(A+C)
展开化简得:2sinAcosC+2cosAsinC=2sinAsinC,
将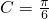 代入,得2sinAcos
代入,得2sinAcos +2cosAsin
+2cosAsin =2sinAsin
=2sinAsin ,
,
∴ sinA+cosA=sinA,即(
sinA+cosA=sinA,即( )sinA=-cosA,
)sinA=-cosA,
所以 .
.
分析:(1)用三角函数的降幂公式结合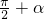 的诱导公式,可得
的诱导公式,可得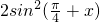 =1+sin2x.代入函数f(x),再用辅助角公式:
=1+sin2x.代入函数f(x),再用辅助角公式: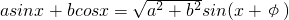 ,进行合并化简得f(x)=
,进行合并化简得f(x)= ,最后可用函数y=Asin(ωx+φ)的周期与单调性的结论与公式,得到函数f(x)的最小正周期和单调增区间.
,最后可用函数y=Asin(ωx+φ)的周期与单调性的结论与公式,得到函数f(x)的最小正周期和单调增区间.
(2)根据函数y=Asin(ωx+φ)的图象变换的规律,先进行相位变换将图象左移,然后再分别进行横坐标和纵坐标的伸缩,可得到函数f(x)= 的变换过程.
的变换过程.
(3根据(1)的表达式,解方程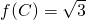 ,结合C为三角形内角,得到
,结合C为三角形内角,得到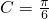 ,将其代入已知等式化简可得(
,将其代入已知等式化简可得( )sinA=-cosA,最后利用同角三角函数的关系,可得 tanA的值.
)sinA=-cosA,最后利用同角三角函数的关系,可得 tanA的值.
点评:本题给出一个特殊的三角函数,结合三角函数的降次公式、诱导公式和辅助角公式,求函数的单调区间与周期,以及求三角函数的值,着重考查了正弦函数的单调性、三角函数的化简求值和函数y=Asin(ωx+φ)的图象变换等知识点,属于中档题.
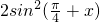 =
=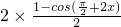 =1-
=1-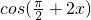 =1+sin2x,
=1+sin2x,∴
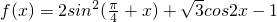 =sin2x+
=sin2x+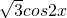 =
=
所以f(x)的最小正周期T=
 =π,
=π,由
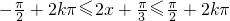 ,解得
,解得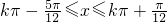
∴函数f(x)的单增区间为[
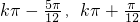 ],k∈Z
],k∈Z(2)函数f(x)的图象可由函数y=sinx的图象先向左平移
 个单位,
个单位,然后将图象上的点纵坐标不变,横坐标缩短为原来的
 ,最后将图象上的点横坐标不变,纵坐标伸长为原来的2倍而得.
,最后将图象上的点横坐标不变,纵坐标伸长为原来的2倍而得.(3)由(1)得
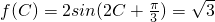 ,所以
,所以
∵0<C<π,
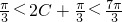 ,
,∴
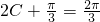 ,可得
,可得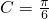 ,
,∵在△ABC中,π-B=A+C,得sinB=sin(A+C)
∴2sinB=cos(A-C)-cos(A+C)可化为:2sin(A+C)=cos(A-C)-cos(A+C)
展开化简得:2sinAcosC+2cosAsinC=2sinAsinC,
将
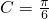 代入,得2sinAcos
代入,得2sinAcos +2cosAsin
+2cosAsin =2sinAsin
=2sinAsin ,
,∴
 sinA+cosA=sinA,即(
sinA+cosA=sinA,即( )sinA=-cosA,
)sinA=-cosA,所以
 .
.分析:(1)用三角函数的降幂公式结合
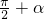 的诱导公式,可得
的诱导公式,可得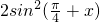 =1+sin2x.代入函数f(x),再用辅助角公式:
=1+sin2x.代入函数f(x),再用辅助角公式: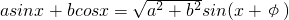 ,进行合并化简得f(x)=
,进行合并化简得f(x)= ,最后可用函数y=Asin(ωx+φ)的周期与单调性的结论与公式,得到函数f(x)的最小正周期和单调增区间.
,最后可用函数y=Asin(ωx+φ)的周期与单调性的结论与公式,得到函数f(x)的最小正周期和单调增区间.(2)根据函数y=Asin(ωx+φ)的图象变换的规律,先进行相位变换将图象左移,然后再分别进行横坐标和纵坐标的伸缩,可得到函数f(x)=
 的变换过程.
的变换过程.(3根据(1)的表达式,解方程
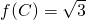 ,结合C为三角形内角,得到
,结合C为三角形内角,得到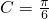 ,将其代入已知等式化简可得(
,将其代入已知等式化简可得( )sinA=-cosA,最后利用同角三角函数的关系,可得 tanA的值.
)sinA=-cosA,最后利用同角三角函数的关系,可得 tanA的值.点评:本题给出一个特殊的三角函数,结合三角函数的降次公式、诱导公式和辅助角公式,求函数的单调区间与周期,以及求三角函数的值,着重考查了正弦函数的单调性、三角函数的化简求值和函数y=Asin(ωx+φ)的图象变换等知识点,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.