题目内容
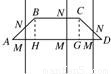
等腰梯形ABCD的两底分别为AD=2a，BC=a，∠BAD=45°，作直线MN⊥AD交AD于M，交折线ABCD于N，若设AM=x，试将梯形ABCD位于直线MN左侧的面积y表示为x的函数，求函数的定义域及表达式，画出流程图.
解：作BH⊥AD，H为垂足，CG⊥AD，G为垂足，依题意，则有AH=
,AG=
a，
(1)当M位于点H的左侧时，N∈AB，
由于AM=x，∠A=45°,
∴MN=x.
∴y=S△AMN=
x2(0≤x≤
).
(2)当M位于HG之间时，
由于AM=x，MN=
，BN=x-
.
∴y=S直角梯形AMNB=
·
［x+(x-
)］=
ax-
(
＜x≤
a).
(3)当M位于点G的右侧时，
由于AM=x，MN=MD=2a-x，
∴y=S梯形ABCD-S△MDN
=
·
(2a+a)-
(2a-x)2
=
-
(4a2-4ax+x2)
=-
x2+2ax-
(
a＜x≤2a).
综上所述,
程序框图如下：
练习册系列答案
相关题目
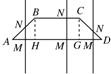等腰梯形ABCD的两底分别为AD=2a，BC=a，∠BAD=45°，作直线MN⊥AD交AD于M，交折线ABCD于N，记AM=x，试将梯形ABCD位于直线MN左侧的面积y表示为x的函数，并写出函数的定义域．
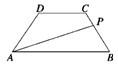等腰梯形ABCD的两底分别为AB=10，CD=4，两腰AD=CB=5，动点P由B点沿折线BCDA向A运动，设P点所经过的路程为x，三角形ABP的面积为S
如图所示，等腰梯形ABCD的两底分别为AD=2，BC=1，∠BAD=45°，直线MN⊥AD交于M，交折线ABCD于N，记AM=x，试将梯形ABCD位于直线MN左侧面积y表示为x的函数，并写出函数的定义域．