Question

已知α、β≠kπ+(k∈Z),且sinθ+cosθ=2sinα,sinθ·cosθ=sin²β,

求证:.

Answer 1

思路解析:比较已知条件和结论,发现结论中没有出现角θ,所以首先要消去它.然后由式子的结构特点,将切化弦统一函数名后分析比较不难得到结论.

证明:因为(sinθ+cosθ)²-2sinθ·cosθ=1,

将已知代入上式得4sin²α-2sin²β=1.                                               ①

另一方面,要证,

即证,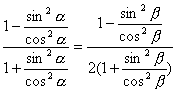

即证cos²α-sin²α=(cos²β-sin²β),

即证1-2sin²α=(1-2sin²β),

即证4sin²α-2sin²β=1.

由于上式与①式相同,于是问题得证.

深化升华  在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q;根据结论的结构特点转化条件,得到中间结论P.若由P可以推出Q成立,就可以证明结论成立.