题目内容
一个盒子里装有4张大小形状完全相同的卡片,分别标有数2,3,4,5;另一个盒子也装有4张大小形状完全相同的卡片,分别标有数3,4,5,6.现从一个盒子中任取一张卡片,其上面的数记为x;再从另一盒子里任取一张卡片,其上面的数记为y,记随机变量η=x+y,求η的分布列和数学期望.
解:随机变量η=x+y,依题意η的可能取值是5,6,7,8,9,10,11
得到P(η=5)= ; P(η=6)=
; P(η=6)=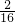
P(η=7)= ; P(η=8)=
; P(η=8)=
P(η=9)= ; P(η=10)=
; P(η=10)=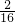
P(η=11)=
∴η的分布列为
∴Eη=5× +6×
+6×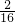 +7×
+7× +8×
+8× +9×
+9× +10×
+10×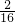 +11×
+11× =8
=8
分析:随机变量η=x+y,依题意η的可能取值是5,6,7,8,9,10,11,结合变量对应的事件,根据相互独立事件同时发生的概率做出概率的值,写出分布列和期望.
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查利用概率知识解决实际问题,本题是一个综合题目.
得到P(η=5)=
 ; P(η=6)=
; P(η=6)=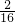
P(η=7)=
 ; P(η=8)=
; P(η=8)=
P(η=9)=
 ; P(η=10)=
; P(η=10)=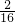
P(η=11)=

∴η的分布列为
| η | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| P |  | 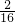 |  |  |  | 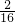 |  |
 +6×
+6×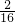 +7×
+7× +8×
+8× +9×
+9× +10×
+10×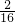 +11×
+11× =8
=8分析:随机变量η=x+y,依题意η的可能取值是5,6,7,8,9,10,11,结合变量对应的事件,根据相互独立事件同时发生的概率做出概率的值,写出分布列和期望.
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查利用概率知识解决实际问题,本题是一个综合题目.

练习册系列答案
相关题目