题目内容
已知函数f(x)=x3-3ax2-9a2x+a3。
(1)设a=1,求函数f(x)的极值;
(2)若a>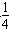 ,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,试确定a的取值范围。
,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,试确定a的取值范围。
(1)设a=1,求函数f(x)的极值;
(2)若a>
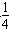 ,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,试确定a的取值范围。
,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,试确定a的取值范围。解:(1)当a=1时,对函数f(x)求导数,得f′(x)=3x2-6x-9
令f′(x)=0,解得x1=-1,x2=3
列表讨论f(x),f′(x)的变化情况:
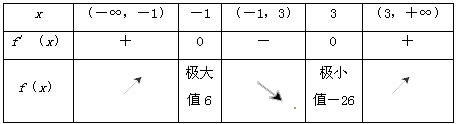
所以,f(x)的极大值是f(-1)=6,极小值是f(3)=-26。
(2)f′(x)=3x2-6ax-9a2的图象是一条开口向上的抛物线,关于x=a对称
若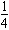 <a≤1,则f′(x)在[1,4a]上是增函数,
<a≤1,则f′(x)在[1,4a]上是增函数,
从而f′(x)在[1,4a]上的最小值是f′(1)=3-6a-9a2,
最大值是f′(4a)=15a2
由|f′(x)|≤12a,得-12a≤3x2-6ax-9a2≤12a,
于是有f′(1)=3-6a-9a2≥-12a,且f′(4a)=15a2≤12a
由f′(1)≥-12a,得-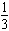 ≤a≤1,
≤a≤1,
由f′(4a)≤12a,得0≤a≤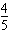 。
。
所以a∈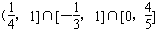
即a∈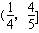
若a>1,则|f′(a)|=12a2>12a
故当x∈[1,4a]时|f′(x)|≤12a不恒成立
所以使|f′(x)|≤12a(x∈[1,4a])恒成立的a的取值范围是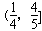 。
。
令f′(x)=0,解得x1=-1,x2=3
列表讨论f(x),f′(x)的变化情况:

所以,f(x)的极大值是f(-1)=6,极小值是f(3)=-26。
(2)f′(x)=3x2-6ax-9a2的图象是一条开口向上的抛物线,关于x=a对称
若
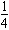 <a≤1,则f′(x)在[1,4a]上是增函数,
<a≤1,则f′(x)在[1,4a]上是增函数,从而f′(x)在[1,4a]上的最小值是f′(1)=3-6a-9a2,
最大值是f′(4a)=15a2
由|f′(x)|≤12a,得-12a≤3x2-6ax-9a2≤12a,
于是有f′(1)=3-6a-9a2≥-12a,且f′(4a)=15a2≤12a
由f′(1)≥-12a,得-
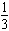 ≤a≤1,
≤a≤1,由f′(4a)≤12a,得0≤a≤
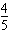 。
。所以a∈
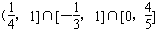
即a∈
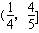
若a>1,则|f′(a)|=12a2>12a
故当x∈[1,4a]时|f′(x)|≤12a不恒成立
所以使|f′(x)|≤12a(x∈[1,4a])恒成立的a的取值范围是
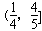 。
。
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|