题目内容
下列判断错误的是( )
A.“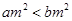 ”是“ ”是“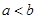 ”的充分不必要条件 ”的充分不必要条件 |
B.“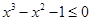 对 对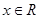 恒成立”的否定是“存在 恒成立”的否定是“存在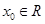 使得 使得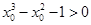 ” ” |
C.若“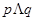 ”为假命题,则 ”为假命题,则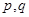 均为假命题 均为假命题 |
D.若随机变量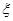 服从二项分布: 服从二项分布: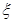 ~ ~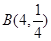 ,则 ,则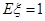 |
C
解析试题分析:对A:“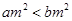 ”成立,则说明
”成立,则说明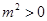 ,所以必有“
,所以必有“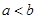 ”,故为充分条件;反之,若“
”,故为充分条件;反之,若“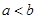 ”,则
”,则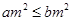 .所以“
.所以“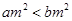 ”是“
”是“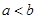 ”的充分不必要条件.
”的充分不必要条件.
对B:全称命题:“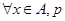 ”的否定为“
”的否定为“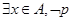 ”.所以“
”.所以“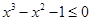 对
对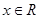 恒成立”的否定是“存在
恒成立”的否定是“存在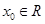 使得
使得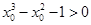 ”,成立.
”,成立.
对C.当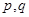 中有一个为假命题时,“
中有一个为假命题时,“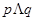 ”就为假命题.所以C不成立.
”就为假命题.所以C不成立.
对D.若随机变量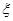 服从二项分布:
服从二项分布: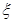 ~
~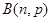 ,则
,则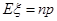 ,所以D正确.
,所以D正确.
考点:逻辑与命题.

练习册系列答案
相关题目
设 是非零向量,已知命题P:若
是非零向量,已知命题P:若 ,
, ,则
,则 ;命题q:若
;命题q:若 ,则
,则 ,则下列命题中真命题是( )
,则下列命题中真命题是( )
A. | B. | C. | D. |
已知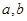 都是实数,那么“
都是实数,那么“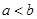 ”是“
”是“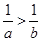 ”的( )条件
”的( )条件
| A.充分不必要 | B.必要不充分 |
| C.充要 | D.既不充分也不必要 |
“ ”是“函数
”是“函数 (
( )在区间
)在区间 上为增函数”的( )
上为增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设平面向量 ,
, ,
, 均为非零向量,则“
均为非零向量,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
已知命题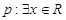 ,
,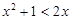 ;命题
;命题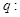 不等式
不等式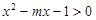 恒成立,那么( )
恒成立,那么( )
A.“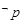 ”是假命题 ”是假命题 | B.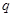 是真命题 是真命题 |
C.“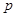 或 或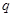 ”为假命题 ”为假命题 | D.“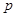 且 且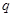 ”为真命题 ”为真命题 |
命题:“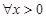 ,都有
,都有 ”的否定是( )
”的否定是( )
A.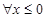 ,都有 ,都有 | B.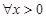 ,都有 ,都有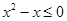 |
C.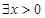 ,使得 ,使得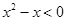 | D.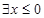 ,使得 ,使得 |
[2013·湖南高考]“1<x<2”是“x<2”成立的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
命题“对任意的x∈R,x3﹣x2+1≤0”的否定是( )
| A.不存在x∈R,x3﹣x2+1≤0 | B.存在x∈R,x3﹣x2+1≤0 |
| C.存在x∈R,x3﹣x2+1>0 | D.对任意的x∈R,x3﹣x2+1>0 |