题目内容
已知向量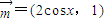 ,向量
,向量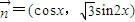 ,
,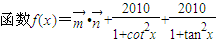 .
.(1)化简f(x)的解析式,并求函数的单调递减区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知f(A)=2012,b=1,△ABC的面积为
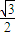 ,求
,求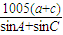 的值.
的值.
【答案】分析:(1)利用两个向量的数量积公式,同角三角函数的基本关系,两角和的正弦公式化简f(x)=2sin(2x+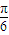 )+2011,
)+2011,
由 2kπ+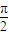 ≤2x+
≤2x+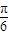 ≤2kπ+
≤2kπ+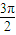 ,且 x≠kπ,x≠kπ+
,且 x≠kπ,x≠kπ+ ,k∈z,求得减区间.
,k∈z,求得减区间.
(2)由f(A)=2012,求得 A,根据△ABC的面积求出c,由余弦定理求出 a,据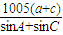 =
=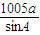 求值.
求值.
解答:解:(1)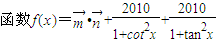 =2cos2x+
=2cos2x+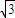 sin2x+
sin2x+
=1+cos2x+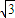 sin2x+2010=2sin(2x+
sin2x+2010=2sin(2x+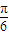 )+2011.
)+2011.
由 2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+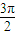 ,且 x≠kπ,x≠kπ+
,且 x≠kπ,x≠kπ+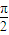 ,k∈z,得 kπ+
,k∈z,得 kπ+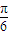 ≤x≤kπ+
≤x≤kπ+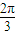 ,且x≠kπ+
,且x≠kπ+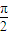 ,
,
∴单调减区间为 (kπ+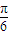 ,kπ+
,kπ+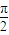 )∪(kπ+
)∪(kπ+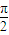 ,kπ+
,kπ+ ).
).
(2)f(A)=2012=2sin(2A+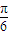 )+2011,∴sin(2A+
)+2011,∴sin(2A+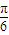 )=
)= ,∴A=
,∴A=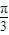 .
.
又△ABC的面积为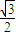 =
= bcsinA=
bcsinA= •1•c•
•1•c•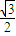 ,∴c=2.
,∴c=2.
∴a=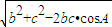 =
=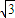 ,∴
,∴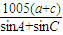 =
=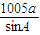 =
=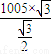 =2010.
=2010.
点评:本题考查两个向量的数量积公式,同角三角函数的基本关系,两角和的正弦公式,余弦定理的应用,求单调减区间是
解题的难点.
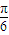 )+2011,
)+2011,由 2kπ+
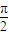 ≤2x+
≤2x+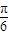 ≤2kπ+
≤2kπ+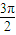 ,且 x≠kπ,x≠kπ+
,且 x≠kπ,x≠kπ+ ,k∈z,求得减区间.
,k∈z,求得减区间.(2)由f(A)=2012,求得 A,根据△ABC的面积求出c,由余弦定理求出 a,据
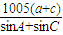 =
=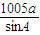 求值.
求值.解答:解:(1)
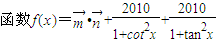 =2cos2x+
=2cos2x+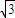 sin2x+
sin2x+
=1+cos2x+
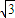 sin2x+2010=2sin(2x+
sin2x+2010=2sin(2x+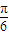 )+2011.
)+2011.由 2kπ+
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+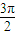 ,且 x≠kπ,x≠kπ+
,且 x≠kπ,x≠kπ+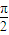 ,k∈z,得 kπ+
,k∈z,得 kπ+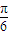 ≤x≤kπ+
≤x≤kπ+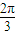 ,且x≠kπ+
,且x≠kπ+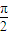 ,
,∴单调减区间为 (kπ+
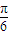 ,kπ+
,kπ+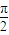 )∪(kπ+
)∪(kπ+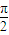 ,kπ+
,kπ+ ).
).(2)f(A)=2012=2sin(2A+
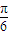 )+2011,∴sin(2A+
)+2011,∴sin(2A+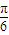 )=
)= ,∴A=
,∴A=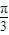 .
.又△ABC的面积为
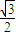 =
= bcsinA=
bcsinA= •1•c•
•1•c•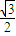 ,∴c=2.
,∴c=2.∴a=
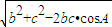 =
=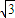 ,∴
,∴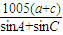 =
=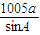 =
=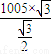 =2010.
=2010.点评:本题考查两个向量的数量积公式,同角三角函数的基本关系,两角和的正弦公式,余弦定理的应用,求单调减区间是
解题的难点.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
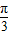 ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于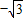
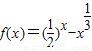 在区间(0,1)上存在零点.
在区间(0,1)上存在零点.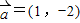 与向量
与向量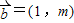 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是(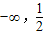 )
) ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于
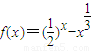 在区间(0,1)上存在零点.
在区间(0,1)上存在零点. 与向量
与向量 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是( )
)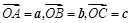 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若
 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算 ,显然
,显然 的结果仍为一向量,记作
的结果仍为一向量,记作 .
. 的法向量;
的法向量; 为边的平行四边形
为边的平行四边形 的面积等于
的面积等于 ;
; 平移,得到一个平行六面体
平移,得到一个平行六面体 ,试判断平行六面体的体积
,试判断平行六面体的体积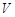 与
与 的大小.
的大小.
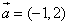 ,点A(8,0),B(n,t),
,点A(8,0),B(n,t),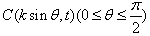 。
。 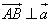 ,且
,且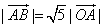 ,求向量
,求向量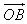 ;
;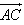 与向量
与向量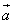 共线,当k>4时,tsinθ的最大值为4,求
共线,当k>4时,tsinθ的最大值为4,求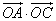 的值。
的值。