题目内容
设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3…若b1>c1,b1+c1=2a1,an+1=an,bn+1=
,cn+1=
,则( )
| cn+an |
| 2 |
| bn+an |
| 2 |
分析:由an+1=an可知△AnBnCn的边BnCn为定值a1,由bn+1+cn+1-2a1=
(bn+cn-2a1)及b1+c1=2a1得bn+cn=2a1,则在△AnBnCn中边长BnCn=a1为定值,另两边AnCn、AnBn的长度之和bn+cn=2a1为定值,
由此可知顶点An在以Bn、Cn为焦点的椭圆上,根据bn+1-cn+1=-
(bn-cn),得bn-cn=(-
)n-1(b1-c1),可知n→+∞时bn→cn,据此可判断△AnBnCn的边BnCn的高hn随着n的增大而增大,再由三角形面积公式可得到答案.
| 1 |
| 2 |
由此可知顶点An在以Bn、Cn为焦点的椭圆上,根据bn+1-cn+1=-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:因为an+1=an,bn+1=
,cn+1=
,所以an=a1,
所以bn+1+cn+1=an+
=a1+
,
所以bn+1+cn+1-2a1=
(bn+cn-2a1),
又b1+c1=2a1,所以bn+cn=2a1,
于是,在△AnBnCn中,边长BnCn=a1为定值,另两边AnCn、AnBn的长度之和bn+cn=2a1为定值,
因为bn+1-cn+1=
-
=-
(bn-cn),
所以bn-cn=(-
)n-1(b1-c1),
当n→+∞时,有bn-cn→0,即bn→cn,
于是△AnBnCn的边BnCn的高hn随着n的增大而增大,
所以其面积Sn=
|BnCn|•hn=
a1hn为递增数列,
故选B.
| cn+an |
| 2 |
| bn+an |
| 2 |
所以bn+1+cn+1=an+
| bn+cn |
| 2 |
| bn+cn |
| 2 |
所以bn+1+cn+1-2a1=
| 1 |
| 2 |
又b1+c1=2a1,所以bn+cn=2a1,
于是,在△AnBnCn中,边长BnCn=a1为定值,另两边AnCn、AnBn的长度之和bn+cn=2a1为定值,
因为bn+1-cn+1=
| cn+an |
| 2 |
| bn+an |
| 2 |
| 1 |
| 2 |
所以bn-cn=(-
| 1 |
| 2 |
当n→+∞时,有bn-cn→0,即bn→cn,
于是△AnBnCn的边BnCn的高hn随着n的增大而增大,
所以其面积Sn=
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查数列、解三角形、椭圆等知识,综合考查学生分析解决问题的能力,有较高的思维抽象度,是本年度全国高考试题中的“亮点”之一.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 ,cn+1=
,cn+1=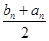 ,则( )
,则( )