题目内容
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上,若圆
在椭圆上,若圆![]() 的一条切线(斜率存在)与椭圆C有两个交点A,B,且
的一条切线(斜率存在)与椭圆C有两个交点A,B,且![]() .
.

(1)求椭圆的标准方程;
(2)求圆O的标准方程;
(3)已知椭圆C的上顶点为M,点N在圆O上,直线MN与椭圆C相交于另一点Q,且![]() ,求直线MN的方程.
,求直线MN的方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据离心率得到![]() ,代入点得到
,代入点得到![]() ,计算得到答案.
,计算得到答案.
(2)设切线方程为![]() ,
,![]() ,
,![]() ,联立方程得到
,联立方程得到![]() ,
,![]() ,根据
,根据![]() 得到
得到![]() ,计算圆心到直线的距离得到答案.
,计算圆心到直线的距离得到答案.
(3)![]() ,设
,设![]() ,
,![]() ,根据
,根据![]() 得到
得到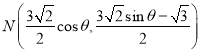 ,代入椭圆得到
,代入椭圆得到![]() ,得到直线方程.
,得到直线方程.
(1)椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
故![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,即
,即![]() .
.
(2)设切线方程为![]() ,
,![]() ,
,![]() ,
,
则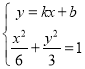 ,化简得到
,化简得到![]() ,
,
故![]() ,
,![]() ,
,
![]() ,
,
代入化简得到:![]() ,验证满足
,验证满足![]() .
.
故![]() ,故圆方程为
,故圆方程为![]() .
.
(3)![]() ,设
,设![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
故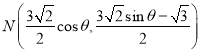 ,
,
代入椭圆方程: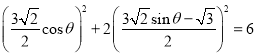 ,化简
,化简![]() ,
,
故![]() ,即
,即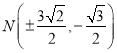 ,故
,故![]() .
.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目