题目内容
已知函数![]() .
.
⑴若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
⑵若![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围.
的取值范围.
.解:⑴![]() ,
,![]() ,又
,又![]() ,所以曲线
,所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() 即
即![]() ,
,
由已知得![]() ,
,![]() ,所以
,所以![]() ,
,![]() .……………………………6分
.……………………………6分
⑵法一、![]()
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上是减函数,在区间
上是减函数,在区间![]() 上也是减函数,…………………8分
上也是减函数,…………………8分
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() ,
,
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函
上是减函![]() 数,
数,![]() 在区间
在区间![]() 上是减函数时,
上是减函数时,![]() ,
,![]() ;……………………………12分
;……………………………12分
综上,![]() 的取值范围是
的取值范围是![]() .……………………………13分
.……………………………13分
法二、![]() ,
,
∵![]() 在区间
在区间![]() 上是减函数,
上是减函数,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
![]() 在区间
在区间![]() 上恒成立,∴
上恒成立,∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
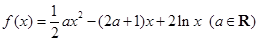 .
. 在
在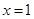 和
和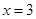 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;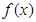 的单调区间;
的单调区间;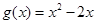 ,若对任意
,若对任意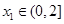 ,均存在
,均存在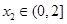 ,使得
,使得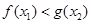 ,求
,求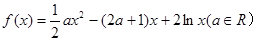
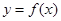 在
在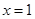 和
和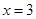 处的切线互相平行,求
处的切线互相平行,求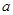 的值及函数
的值及函数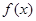 的单调区间;
的单调区间;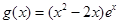 ,若对任意
,若对任意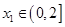 ,均存在
,均存在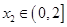 ,使得
,使得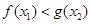 ,求实数
,求实数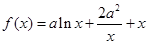 .
.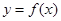 在点
在点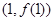 处的切线与直线
处的切线与直线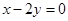 垂直,求实数
垂直,求实数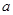 的值.
的值.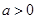 ,求
,求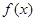 的最小值
的最小值 ;
;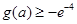 .
.
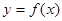 在
在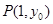 处的切线平行于直线
处的切线平行于直线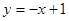 ,求函数
,求函数 ,且对
,且对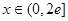 时,
时,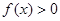 恒成立,求实数
恒成立,求实数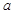 的取值范围.
的取值范围.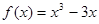 ,若曲线
,若曲线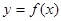 在点A(0,16)处的切线方程为
在点A(0,16)处的切线方程为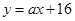 ,则实数
,则实数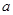 的值是( )
的值是( )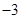 B.
B.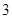 C.6
D.9
C.6
D.9