题目内容
12.已知A={x|x2-5x+6<0},B={x|x2-4ax+a2≤0}(a>0),且A⊆B,试求实数a的取值范围.分析 化简集合A={x|x2-5x+6<0},根据集合包含关系的定义,可构造一个关于a的不等式组,解不等式组,可得实数a的取值范围.
解答 解:集合A={x|x2-5x+6<0}=(2,3),
若A⊆B,则必有$\left\{\begin{array}{l}{4-8a+{a}^{2}≤0}\\{9-12a+{a}^{2}≤0}\end{array}\right.$
解得6-3$\sqrt{3}$≤a≤4+2$\sqrt{3}$.
点评 本题考查的知识点是集合关系中的参数取值问题,其中根据已知条件,构造关于a的不等式组,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的左焦点为F,右顶点为A,点P在椭圆上,直线AP交y轴于点M,若$\overrightarrow{PF}$=$\sqrt{3}\overrightarrow{MO}$(O为坐标原点),则椭圆的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{3}-1$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{3}$ |
3.设x,y满足约束条件$\left\{\begin{array}{l}{x-2y≥-2}\\{3x-2y≤3}\\{x+y≥1}\end{array}\right.$,若x2+4y2≥m恒成立,则实数m的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
17.“α≠2kπ+$\frac{π}{2}$(k∈Z)”是“tanα=$\frac{sinα}{cosα}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.把正整数1,2,3,4,5,6,…按某种规律填入下表:
按照这种规律继续填写,那么2015出现在( )
| 2 | 6 | 10 | 14 | ||||||||
| 1 | 4 | 5 | 8 | 9 | 12 | 13 | …. | ||||
| 3 | 7 | 11 | 15 |
| A. | 第1行第1510列 | B. | 第3行第1510列 | C. | 第2行第1511列 | D. | 第3行第1511列 |
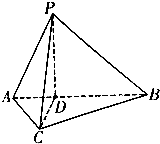 如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.
如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.