题目内容
若f(2)=a23+b2
+1，且f（4）=5，则f（-4）=______．
| 1 |
| 3 |
设g（三）=a三3+b三
则有f（三）=g（三）+1
∵f（2）=5∴g（2）=e即g（2）=8a+2
b=e
∵g（-三）=-（a三3+b三
）=g（三）
∴g（三）是R上的奇函数
所以g（-2）=-e
∴f（-2）=g（-2）+1=-3
∴f（-2）=-3
故答案为-3．
| 1 |
| 3 |
∵f（2）=5∴g（2）=e即g（2）=8a+2
| 1 |
| 3 |
∵g（-三）=-（a三3+b三
| 1 |
| 3 |
∴g（三）是R上的奇函数
所以g（-2）=-e
∴f（-2）=g（-2）+1=-3
∴f（-2）=-3
故答案为-3．
练习册系列答案
同步练习强化拓展系列答案
相关题目
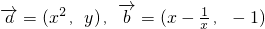，且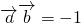
．如果存在正项数列{an}满足：
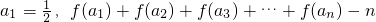=a13+a23+a33+…+an3-n2an（n∈N*）．
．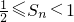