已知数列{an}的首项a1=1,其前n项和Sn与an之间满足an=(n≥2).(1)求证:数列{}为等差数列;(2)求数列{an}的通项公式. 题目和参考答案——青夏教育精英家教网——

题目内容

已知数列{a_n}的首项a₁=1,其前n项和S_n与a_n之间满足a_n=(n≥2).

(1)求证:数列{}为等差数列;

(2)求数列{a_n}的通项公式.

(1)证明:∵a_n=S_n－S_n_－1，由已知条件知

S_n－S_n_－1=.整理得－=2(n≥2),

∴{}构成等差数列.

(2)解:∵S₁=a₁=1,由(1)得=+2(n－1),即=2n－1.

∴S_n=.

当n≥2时，a_n=S_n－S_n_－1=－=,

∴a_n=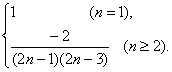

点评:已知a_n和S_n之间的关系，求数列{a_n}的通项公式，可先求S_n，再通过S_n求a_n，在已知S_n求a_n的过程中，要注意数列的首项.

练习册系列答案

全优中考系统总复习系列答案

全优卷练考通系列答案

全优点练单元计划系列答案

全优标准卷系列答案

全能课堂系列答案

全能超越堂堂清课堂8分钟小测系列答案

全练练测考系列答案

招生分班真题分类卷系列答案

全程助学系列答案

全程提优大考卷系列答案

相关题目

已知数列{a_n}的首项a₁=

，前n项和S_n=n²a_n（n≥1）．
（1）求数列{a_n}的通项公式；
（2）设b₁=0，b_n=

(n≥2)，T_n为数列{b_n}的前n项和，求证：Tn＜

已知数列{a_n}的首项为a₁=2，前n项和为S_n，且对任意的n∈N^*，当n≥2，时，a_n总是3S_n-4与2-

Sn-1的等差中项．
（1）求数列{a_n}的通项公式；
（2）设b_n=（n+1）a_n，T_n是数列{b_n}的前n项和，n∈N^*，求T_n．

（2013•江门一模）已知数列{a_n}的首项a₁=1，若?n∈N^*，a_n•a_n+1=-2，则a_n=

1，n是正奇数

-2，n是正偶数

1，n是正奇数

-2，n是正偶数

已知数列{a_n}的首项为a₁=3，通项a_n与前n项和s_n之间满足2a_n=S_n•S_n-1（n≥2）．
（1）求证：数列{

}是等差数列；
（2）求数列{a_n}的通项公式；
（3）求数列{a_n}中的最大项．

已知数列{a_n}的首项a1=

，n∈N⁺
（Ⅰ）设bn=

-1证明：数列{b_n}是等比数列；
（Ⅱ）数列{

}的前n项和S_n．