题目内容
6.等比数列{an}满足a1+a3=10,a2+a4=5,则an=24-n.分析 由等比数列性质列出方程组,求出a1=8,q=$\frac{1}{2}$,由此能求出an.
解答 解:∵等比数列{an}满足a1+a3=10,a2+a4=5,
∴$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}{q}^{2}=10}\\{{a}_{1}q+{a}_{1}{q}^{3}=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=8}\\{q=\frac{1}{2}}\end{array}\right.$,
∴an=8×($\frac{1}{2}$)n-1=24-n.
故答案是:24-n.
点评 本题考查等比数列的第8项的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的体积是( )
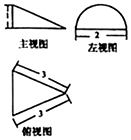

| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{π}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}π$ | D. | π |
18.直线x-y+4=0被圆x2+y2+4x-4y+6=0截得的弦长等于( )
| A. | 8 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
15.8把椅子摆成一排,4人随机就座,任何两人不相邻的坐法种数为( )
| A. | 144 | B. | 120 | C. | 72 | D. | 24 |
16.某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量y与年份x之间的回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)预测该地2018年的商品需求量(结果保留整数).
| 年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
| 需要量(万件) | 236 | 246 | 257 | 276 | 286 |
(2)预测该地2018年的商品需求量(结果保留整数).
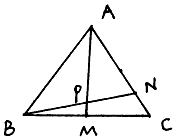 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=3NC,AM与BN相交于点P,设$\overrightarrow{CA}$=$\overrightarrow a$,$\overrightarrow{CB}$=$\overrightarrow b$,用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{CP}$.
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=3NC,AM与BN相交于点P,设$\overrightarrow{CA}$=$\overrightarrow a$,$\overrightarrow{CB}$=$\overrightarrow b$,用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{CP}$.