题目内容
 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,底面ABCD为正方形,且PD=AD,点E和点F分别是PB和CD的中点,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,底面ABCD为正方形,且PD=AD,点E和点F分别是PB和CD的中点,PH为△PAD中AD边上的高.(1)证明:PH⊥平面ABCD;
(2)证明:平面PBF⊥平面PAB.
分析:(1)根据AB⊥面PAD结合线面垂直的性质可得AB⊥PH,结合PH为△PAD中AD边上的高及线面垂直的判定定理,可得PH⊥平面ABCD;
(2)取PA中点G,连接DG,GE,可证得四边形DGEF为平行四边形,根据等腰三角形三线合一可得DG⊥PA,再由(1)中结论及线面垂直的判定定理可证DG⊥平面PAB,由线面垂直的第二判定定理可得EF⊥平面PAB,最后由面面垂直的判定定理得到答案.
(2)取PA中点G,连接DG,GE,可证得四边形DGEF为平行四边形,根据等腰三角形三线合一可得DG⊥PA,再由(1)中结论及线面垂直的判定定理可证DG⊥平面PAB,由线面垂直的第二判定定理可得EF⊥平面PAB,最后由面面垂直的判定定理得到答案.
解答:证明:(1)∵AB⊥面PAD,PH?面PAD,
∴AB⊥PH,
又∵PH⊥AD,AB?平面ABCD,AD?平面ABCD,AB∩AD=A,
∴PH⊥平面ABCD;
(2)取PA中点G,连接DG,GE,
又∵DF=
CD,DF∥CD,CD=AB,
∴GE=DF且GE∥DF,即四边形DGEF为平行四边形,
∴EF∥DG,
∵DP=DA
∴DG⊥PA,
又∵AB⊥平面PAD,DG?平面PAD
∴AB⊥GD,
又∵PA∩AB=A,PA?平面PAB,AB?平面PAB,
∴DG⊥平面PAB,
∵DG∥EF,
∴EF⊥平面PAB,
又∵EF?平面PBF
∴平面PBF⊥平面PAB.
∴AB⊥PH,
又∵PH⊥AD,AB?平面ABCD,AD?平面ABCD,AB∩AD=A,
∴PH⊥平面ABCD;
(2)取PA中点G,连接DG,GE,
|
又∵DF=
| 1 |
| 2 |
∴GE=DF且GE∥DF,即四边形DGEF为平行四边形,
∴EF∥DG,
∵DP=DA
∴DG⊥PA,
又∵AB⊥平面PAD,DG?平面PAD
∴AB⊥GD,
又∵PA∩AB=A,PA?平面PAB,AB?平面PAB,
∴DG⊥平面PAB,
∵DG∥EF,
∴EF⊥平面PAB,
又∵EF?平面PBF
∴平面PBF⊥平面PAB.
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面垂直的判定,熟练掌握空间线线垂直,线面垂直及在面垂直之间的相互转化是解答的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
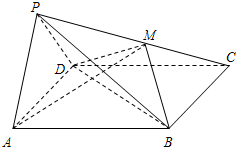 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.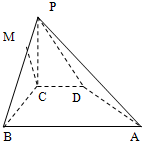 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB