题目内容
1.函数f(x)=x+$\frac{4}{x-3}$,x∈(3,+∞)的最小值为( )| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
分析 求出x-3的范围,根据基本不等式的性质求出f(x)的最小值即可.
解答 解:∵x>3,∴x-3>0,
∴f(x)=x+$\frac{4}{x-3}$=(x-3)+$\frac{4}{x-3}$+3≥2$\sqrt{(x-3)•\frac{4}{x-3}}$+3=7,
当且仅当x-3=$\frac{4}{x-3}$即x=5时”=“成立,
故f(x)的最小值是7,
故选:D.
点评 本题考查了基本不等式的性质,注意应用不等式需满足的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下面的伪代码输出的结果S为( )
I←1
While I<8
I←I+2
S←2I+3
End while
Print S.
I←1
While I<8
I←I+2
S←2I+3
End while
Print S.
| A. | 17 | B. | 19 | C. | 21 | D. | 23 |
12.已知三角形ABC内的一点D满足$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$•$\overrightarrow{DC$=$\overrightarrow{DC}$•$\overrightarrow{DA}$=-2,且|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|.平面ABC内的动点P,M满足|$\overrightarrow{AP}$|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则|$\overrightarrow{BM}$|2的最大值是( )
| A. | $\frac{49}{4}$ | B. | $\frac{43}{4}$ | C. | $\frac{{37+6\sqrt{3}}}{4}$ | D. | $\frac{{37+2\sqrt{33}}}{4}$ |
9.设函数f(x)=-4x+2x+1-1,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (0,4] | B. | (-∞,4] | C. | (-4,0] | D. | [4,+∞) |
10.执行如图所示的程序框图,若输出的S=183,则判断框内应填入的条件是( )
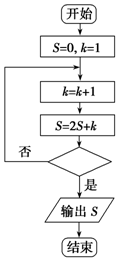

| A. | k>7? | B. | k>6? | C. | k>5? | D. | k>4? |
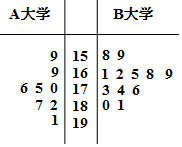 某市旅游节需在A大学和B大学中分别招募8名和12名志愿者,这20名志愿者的身高(单位:cm)绘制出如图所示的茎叶图.若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”.
某市旅游节需在A大学和B大学中分别招募8名和12名志愿者,这20名志愿者的身高(单位:cm)绘制出如图所示的茎叶图.若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”.