题目内容

已知椭圆9x²+16y²=144，焦点为F₁、F₂，P是椭圆上一点，且∠F₁PF₂=60°，则 $数学公式$ =________．

$\text{[math]}$
分析：将椭圆9x²+16y²=144化成标准形式，从而得到a²=16，b²=9，所以c= $\text{[math]}$ = $\text{[math]}$ ．再根据椭圆的定义得到|PF₁|+
|PF₂|=2a=8；以及△F₁PF₂中利用余弦定理，得到|PF₁|²+|PF₂|²-2|PF₁||PF₂|cos60°=28．两式联解，可得|PF₁|•
|PF₂|=12，最后用面积正弦定理公式，可以求出△F₁PF₂的面积．
解答：将椭圆9x²+16y²=144化成标准形式： $\text{[math]}$ ，
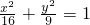∴a²=16，b²=9
∴c= $\text{[math]}$ = $\text{[math]}$ ．
设|PF₁|=r₁，|PF₂|=r₂，
则由椭圆的定义可得：r₁+r₂=8①
在△F₁PF₂中∠F₁PF₂=60°，
根据余弦定理，得：r₁²+r₂²-2r₁r₂cos60°=28②，
由①²-②，得r₁r₂=12，
∴ $\text{[math]}$ ，
故答案为： $\text{[math]}$ ．
点评：本题在椭圆中给出一点，它到两个焦点的张角为特殊角，通过求焦点三角形的面积，考查了椭圆的基本概念和正、余弦定理等知识点，属于中档题．