题目内容
已知随机变量ξ的分布律如下:
其中a,b,c成等差数列,若ξ的均值E(ξ)=
,则ξ的方差D(ξ)等于( )
| x | 0 | 1 | 2 |
| P(ξ=x) | a | b | c |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据a,b,c成等差数列,ξ的均值E(ξ)=
,求出a,b,c的值,利用期望与方差的公式,计算即可.
| 4 |
| 3 |
解答:解:∵a,b,c成等差数列,∴a+c=2b,
又∵a+b+c=1,
∴b=
;
又∵P(ξ)=0×a+1×
+2×c=
+2c=
,
∴c=
;
∴a=
,
∴ξ的方差为
D(ξ)=(0-
)2×
+(1-
)2×
+(2-
)2×
=
.
故选:C.
又∵a+b+c=1,
∴b=
| 1 |
| 3 |
又∵P(ξ)=0×a+1×
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∴c=
| 1 |
| 2 |
∴a=
| 1 |
| 6 |
∴ξ的方差为
D(ξ)=(0-
| 4 |
| 3 |
| 1 |
| 6 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 5 |
| 9 |
故选:C.
点评:本题考查了求离散型随机变量的期望与方差的问题,解题时应先求出a,b,c的值,利用期望与方差的公式,直接计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
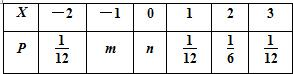 已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=
已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|