题目内容
(本题满分16分)
设 为实数,且
为实数,且
(1)求方程 的解;
的解;
(2)若 ,
,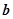 满足
满足 ,试写出
,试写出 与
与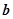 的等量关系(至少写出两个);
的等量关系(至少写出两个);
(3)在(2)的基础上,证明在这一关系中存在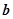 满足
满足 .
.
【答案】
解:(1)由 得,
得, 所以
所以 ……………………..4分
……………………..4分

(2)结合函数图像,由 可判断
可判断
 ,……………………..5分
,……………………..5分
从而 ,从而
,从而 ……………..6分
……………..6分
又 ,……………………..7分
,……………………..7分
因为 ,所以
,所以 ……………………..8分
……………………..8分
从而由
可得 ,……………………..9分
,……………………..9分
从而 ……………………..10分
……………………..10分
(3)由
得 ……………………..11分
……………………..11分
 ……………………..12分
……………………..12分
令 ,……………………..14分
,……………………..14分
因为 ,根据零点存在性定理可知,……………………..15分
,根据零点存在性定理可知,……………………..15分
函数 在
在 内一定存在零点,
内一定存在零点,
即方程 存在
存在 的根。……………………..16分
的根。……………………..16分
【解析】略

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在