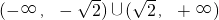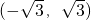题目内容
若坐标原点在圆(x-m)2+(y+m)2=4的内部,则实数m的取值范围是( )
| A、-1<m<1 | ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
分析:直接将原点的坐标代入圆方程的左边,可得左边小于右边,解之即可得到实数m的取值范围.
解答:解:∵原点O在圆(x-m)2+(y+m)2=4的内部,
∴(0-m)2+(0+m)2<4,
得2m2<4,
解得-
<m<
即实数m的取值范围为:-
<m<
.
故选:C.
∴(0-m)2+(0+m)2<4,
得2m2<4,
解得-
| 2 |
| 2 |
即实数m的取值范围为:-
| 2 |
| 2 |
故选:C.
点评:本题着重考查了圆的方程和点与圆的位置关系等知识,点在圆上则点的坐标适合方程,点在圆外则点的坐标代入方程是大于号,点在圆内则点的坐标代入方程是小于号,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目