题目内容
将甲桶中的a升水缓慢注入空桶乙中,tmin后甲桶中剩余的水符合指数衰减曲线y=aent,若5min后甲桶和乙桶的水量相等,又过了mmin后甲桶中的水只有
升,则m=
| a | 8 |
10
10
.分析:由题意,函数y=f(t)=aent满足f(5)=
a,解出n=
ln
.再根据f(m)=
a,建立关于m的指数方程,由对数恒成立化简整理,即可解出m的值.
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 8 |
解答:解:根据题意,得
∵5min后甲桶和乙桶的水量相等,
∴函数y=f(t)=aent,满足f(5)=ae5n=
a
可得n=
ln
因此,当kmin后甲桶中的水只有
升,即f(k)=
a
即
ln(
•k)=ln
,
ln(
•k)=3ln
,解之得k=15,
经过了k-5=10分钟,即m=10
故答案为:10
∵5min后甲桶和乙桶的水量相等,
∴函数y=f(t)=aent,满足f(5)=ae5n=
| 1 |
| 2 |
可得n=
| 1 |
| 5 |
| 1 |
| 2 |
因此,当kmin后甲桶中的水只有
| a |
| 8 |
| 1 |
| 8 |
即
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
经过了k-5=10分钟,即m=10
故答案为:10
点评:本题给出实际应用问题,求经过几分钟后桶内的水量剩余八分之一.着重考查了指数函数的性质、指数恒等式化简指数方程和对数的运算性质等知识,属于中档题.

练习册系列答案
相关题目
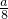 升,则m=________.
升,则m=________. 升,则m= .
升,则m= .