题目内容
13.在空间中,a,b是不重合的直线,α,β是不重合的平面,则下列条件可推出a∥b的是( )| A. | a?α,b?β,α∥β | B. | a∥α,b?β | C. | a⊥α,b⊥α | D. | a⊥α,b?α |
分析 A中,根据面面平行的几何特征,可判断出与b没有公共点,但a与b可能平行或异面
B中,根据线面平行的几何特征,可判断出与b没有公共点,但a与b可能平行或异面
C中,根据线面垂直的性质定理可得a∥b
D中,根据线面垂直的定义可得a⊥b.
解答 解:对于A,若a?α,b?β,α∥β,则a与b没有公共点,即a与b平行或异面;
对于B,若a∥α,b?α,则a与b没有公共点,即a与b平行或异面;
对于C,若a⊥α,b⊥α,由线面垂直的性质定理,可得a∥b;
对于D,若a⊥α,b?α,则由线面垂直的定义可得a⊥b;
故选:C.
点评 本题考查的知识点是空间中直线与直线之间的位置关系及直线与平面之间的位置关系,熟练掌握空间线面关系的判定及几何特征是解答的关键.

练习册系列答案
相关题目
3.执行图中程序框图,如果输入x1=2,x2=3,x3=7,则输出的T值为( )


| A. | 0 | B. | 4 | C. | 2 | D. | 3 |
4.若函数f( x)=ax3-bx+c为奇函数,则c=( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
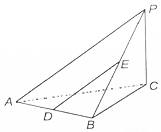 如图,在三棱锥P-ABC中,PC⊥底面ABC,△ABC为等腰直角三角形,∠ABC=90°,D,E分别是AB,PB的中点.
如图,在三棱锥P-ABC中,PC⊥底面ABC,△ABC为等腰直角三角形,∠ABC=90°,D,E分别是AB,PB的中点.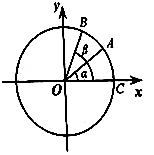 如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).
如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).