题目内容
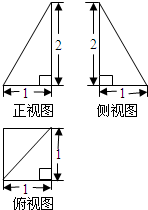
一空间几何体的三视图如图所示,则该几何体的体积为( )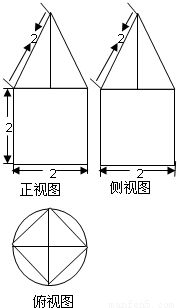
A.2π+2
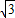
B.4π+2
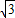
C.2π+
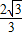
D.4π+
【答案】分析:由三视图及题设条件知,此几何体为一个上部是四棱锥,下部是圆柱其高已知,底面是半径为1的圆,故分别求出两个几何体的体积,再相加既得组合体的体积.
解答:解:此几何体为一个上部是正四棱锥,下部是圆柱
由于圆柱的底面半径为1,其高为2,故其体积为π×12×2=2π
棱锥底面是对角线为2的正方形,故其边长为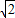 ,其底面积为2,又母线长为2,
,其底面积为2,又母线长为2,
故其高为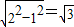
由此知其体积为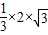 =
=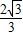
故组合体的体积为2π+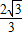
故选C
点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是组合体的体积,其方法是分部来求,再求总体积.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.
解答:解:此几何体为一个上部是正四棱锥,下部是圆柱
由于圆柱的底面半径为1,其高为2,故其体积为π×12×2=2π
棱锥底面是对角线为2的正方形,故其边长为
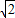 ,其底面积为2,又母线长为2,
,其底面积为2,又母线长为2,故其高为
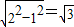
由此知其体积为
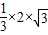 =
=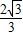
故组合体的体积为2π+
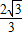
故选C
点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是组合体的体积,其方法是分部来求,再求总体积.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
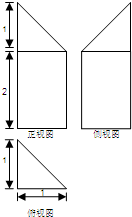
 (2013•成都一模)一空间几何体的三视图如图所示,图中各线段旁的数字表示 该线段的长度,则该几何体的体积为( )
(2013•成都一模)一空间几何体的三视图如图所示,图中各线段旁的数字表示 该线段的长度,则该几何体的体积为( ) (2013•德州一模)一空间几何体的三视图如图所示,该几何体的体积为
(2013•德州一模)一空间几何体的三视图如图所示,该几何体的体积为 (2012•厦门模拟)已知一空间几何体的三视图如图所示,则该几何体中相互垂直的棱共有( )
(2012•厦门模拟)已知一空间几何体的三视图如图所示,则该几何体中相互垂直的棱共有( )