题目内容
已知定义在正实数集上的函数f(x)＝
x2＋2ax，g(x)＝3a2lnx＋b，其中a>0，设两曲线y＝f(x)，y＝g(x)有公共点，且在该点处的切线相同．
(1)用a表示b；
(2)求F(x)＝f(x)－g(x)的极值；
(3)求b的最大值．
解析 (1)设y＝f(x)与y＝g(x)的公共点为(x0，y0)．
∵f′(x)＝x＋2a，g′(x)＝
，由题意f(x0)＝g(x0)，f′(x0)＝g′(x0)．
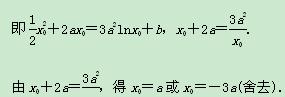即有
(2
则F′
．
所以F(x)在(0，a)上为减函数，在(a，＋∞)上为增函数．
于是函数F(x)在x＝a时有极小值，
F(x)极小＝F(a)＝F(x0)＝f(x0)－g(x0)＝0，
F(x)＝f(x)－g(x)＝x2
＋2ax－3a2lnx－b(x>0)无极大值．
(3)由(1)知令h(t)＝
t2－3t2lnt(t>0)，
则h′(t)＝2t(1－3lnt)．
当t(1－3lnt)>0，即
，h′(t)>0；
当t(1－3lnt)<0，即
时，h′(t)<0.
故h(t)在(
)为增函数，在(
)为减函数．
于是h(t)在(0，＋∞)上的极大值即为最大值：
.
即b的最大值为
.
练习册系列答案
相关题目