题目内容
【题目】2019年12月份,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了增强居民防护意识,增加居民防护知识,某居委会利用网络举办社区线上预防新冠肺炎知识答题比赛,所有居民都参与了防护知识网上答卷,最终甲、乙两人得分最高进入决赛,该社区设计了一个决赛方案:①甲、乙两人各自从![]() 个问题中随机抽
个问题中随机抽![]() 个.已知这
个.已知这![]() 个问题中,甲能正确回答其中的
个问题中,甲能正确回答其中的![]() 个,而乙能正确回答每个问题的概率均为
个,而乙能正确回答每个问题的概率均为![]() ,甲、乙两人对每个问题的回答相互独立、互不影响;②答对题目个数多的人获胜,若两人答对题目数相同,则由乙再从剩下的
,甲、乙两人对每个问题的回答相互独立、互不影响;②答对题目个数多的人获胜,若两人答对题目数相同,则由乙再从剩下的![]() 道题中选一道作答,答对则判乙胜,答错则判甲胜.
道题中选一道作答,答对则判乙胜,答错则判甲胜.
(1)求甲、乙两人共答对![]() 个问题的概率;
个问题的概率;
(2)试判断甲、乙谁更有可能获胜?并说明理由;
(3)求乙答对题目数的分布列和期望.
【答案】(1)![]() (2)乙胜出的可能性更大,详见解析(3)分布列见解析;期望为
(2)乙胜出的可能性更大,详见解析(3)分布列见解析;期望为![]()
【解析】
(1)利用互斥事件概率加法公式、![]() 次独立重复试验中事件
次独立重复试验中事件![]() 恰好发生
恰好发生![]() 次概率计算公式能求出甲、乙两名学生共答对2个问题的概率.
次概率计算公式能求出甲、乙两名学生共答对2个问题的概率.
(2)设甲获胜为事件,则事件包含“两人共答![]() 题甲获胜”和“两人共答
题甲获胜”和“两人共答![]() 题甲获胜”两类情况,其中第一类包括甲乙答对题个数比为
题甲获胜”两类情况,其中第一类包括甲乙答对题个数比为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六种情况,第二类包括前三题甲乙答对题个数比为
六种情况,第二类包括前三题甲乙答对题个数比为![]() ,
,![]() ,
,![]() 三种情况,计算出甲获胜的概率,再根据对立事件的概率公式求出乙获胜的概率即可判断;
三种情况,计算出甲获胜的概率,再根据对立事件的概率公式求出乙获胜的概率即可判断;
(3)设学生乙答对的题数为![]() ,则
,则![]() 的所有可能取值为
的所有可能取值为![]() ,计算出相应的概率,列出分布列,即可求出数学期望;
,计算出相应的概率,列出分布列,即可求出数学期望;
(1)甲、乙共答对![]() 个问题分别为:两人共答
个问题分别为:两人共答![]() 题,甲答对
题,甲答对![]() 个,乙答对
个,乙答对![]() 个;两人共答
个;两人共答![]() 题,甲答对
题,甲答对![]() 个,乙答对
个,乙答对![]() 个.
个.
所以甲、乙两保学生共答对![]() 个问题的概率:
个问题的概率:
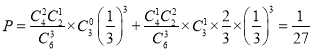 .
.
(2)设甲获胜为事件,则事件包含“两人共答![]() 题甲获胜”和“两人共答
题甲获胜”和“两人共答![]() 题甲获胜”两类情况,其中第一类包括甲乙答对题个数比为
题甲获胜”两类情况,其中第一类包括甲乙答对题个数比为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六种情况,第二类包括前三题甲乙答对题个数比为
六种情况,第二类包括前三题甲乙答对题个数比为![]() ,
,![]() ,
,![]() 三种情况,所以甲获胜的概率
三种情况,所以甲获胜的概率
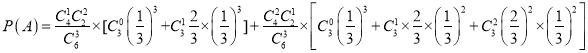
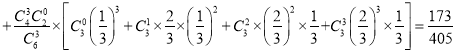 ,
,
设乙获胜为事件![]() ,则
,则![]() 为对立事件,
为对立事件,
所以![]() ,
,![]()
所以乙胜出的可能性更大.
(3)设学生乙答对的题数为![]() ,则
,则![]() 的所有可能取值为
的所有可能取值为![]() ,
,

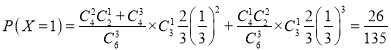
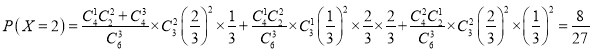
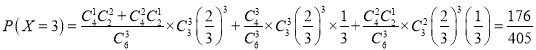
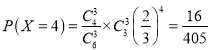
所以随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
所以期望![]() .
.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案