题目内容
在△ABC中，求分别满足下列条件的三角形形状：
①B=60°，b2=ac；②b2tanA=a2tanB；
③sinC=
；④（a2-b2）sin（A+B）=（a2+b2）sin（A-B）．
①B=60°，b2=ac；②b2tanA=a2tanB；
③sinC=
| sinA+sinB |
| cosA+cosB |
①由余弦定理cos60°=
?
=
?a2+c2-ac=ac
∴（a-c）2=0，∴a=c．由a=c及B=60°可知△ABC为等边三角形．
②由b2tanA=a2tanB?
=
?
=
=
∴sinAcosA=sinBcosB，∴sin2A=sin2B，∴A=B或A+B=90°，
∴△ABC为等腰△或Rt△．
③∵sinC=
，由正弦定理：c（cosA+cosB）=a+b，
再由余弦定理：c×
+c×
=a+b
∴（a+b）（c2-a2-b2）=0，∴c2=a2+b2，∴△ABC为Rt△．
④由条件变形为
=
∴
=
，?
=
，∴sin2A=sin2B，∴A=B或A+B=90°．
∴△ABC是等腰△或Rt△．
| a2+c2-b2 |
| 2ac |
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∴（a-c）2=0，∴a=c．由a=c及B=60°可知△ABC为等边三角形．
②由b2tanA=a2tanB?
| b2sinA |
| cosA |
| a2sinB |
| cosB |
| sinBcosA |
| sinAcosB |
| b2 |
| a2 |
| sin2B |
| sin2A |
∴△ABC为等腰△或Rt△．
③∵sinC=
| sinA+sinB |
| cosA+cosB |
再由余弦定理：c×
| a2+b2-c2 |
| 2bc |
| a2+c2-b2 |
| 2ac |
∴（a+b）（c2-a2-b2）=0，∴c2=a2+b2，∴△ABC为Rt△．
④由条件变形为
| sin(A-B) |
| sin(A+B) |
| a2-b2 |
| a2+b2 |
∴
| sin(A+B)+sin(A-B) |
| sin(A+B)-sin(A-B) |
| a2 |
| b2 |
| sinAcosB |
| cosAsinB |
| sin2A |
| sin2B |
∴△ABC是等腰△或Rt△．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
．
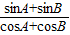