题目内容
正三棱锥P-ABC的底面边长为 ,侧棱PA=a,则二面角P-AB-C的大小是________.
,侧棱PA=a,则二面角P-AB-C的大小是________.
arccos
分析:取AB的中点为D,再连接PD,CD,由题意可得:PD⊥AB,CD⊥AB,可得∠PDC是二面角P-AB-C的平面角.结合题中的条件可得:在△PDC中,有PD=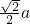 ,CD=
,CD= ,PC=a,
,PC=a,
进而结合余弦定理可得答案.
解答: 解:取AB的中点为D,再连接PD,CD,
解:取AB的中点为D,再连接PD,CD,
因为棱锥P-ABC为正三棱锥,即PA=PB,AC=BC,
所以PD⊥AB,CD⊥AB,
所以∠PDC是二面角P-AB-C的平面角,即为所求角.
因为正三棱锥P-ABC的底面边长为 ,侧棱PA=a,
,侧棱PA=a,
所以PD=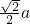 ,CD=
,CD= ,
,
在△PDC中,有PD=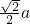 ,CD=
,CD= ,PC=a,
,PC=a,
所以由余弦定理可得:cos∠PDC= ,
,
所以二面角P-AB-C的大小是arccos .
.
故答案为:arccos .
.
点评:本题主要考查二面角的平面角,解决此类问题的步骤是:找角,证角,求角三步,其中根据二面角平面角的定义找角是解决问题的关键,此题属于中档题.

分析:取AB的中点为D,再连接PD,CD,由题意可得:PD⊥AB,CD⊥AB,可得∠PDC是二面角P-AB-C的平面角.结合题中的条件可得:在△PDC中,有PD=
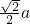 ,CD=
,CD= ,PC=a,
,PC=a,进而结合余弦定理可得答案.
解答:
 解:取AB的中点为D,再连接PD,CD,
解:取AB的中点为D,再连接PD,CD,因为棱锥P-ABC为正三棱锥,即PA=PB,AC=BC,
所以PD⊥AB,CD⊥AB,
所以∠PDC是二面角P-AB-C的平面角,即为所求角.
因为正三棱锥P-ABC的底面边长为
 ,侧棱PA=a,
,侧棱PA=a,所以PD=
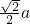 ,CD=
,CD= ,
,在△PDC中,有PD=
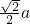 ,CD=
,CD= ,PC=a,
,PC=a,所以由余弦定理可得:cos∠PDC=
 ,
,所以二面角P-AB-C的大小是arccos
 .
.故答案为:arccos
 .
.点评:本题主要考查二面角的平面角,解决此类问题的步骤是:找角,证角,求角三步,其中根据二面角平面角的定义找角是解决问题的关键,此题属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目