题目内容
设O是正三棱锥P-ABC的底面△ABC的中心,过O的动平面与PC交于S,与PA、PB的延长线分别交于Q、R,则
+
+
( )
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| PS |
分析:设正三棱锥P-ABC中,各侧棱两两夹角为α,PC与面PAB所成角为β,则vS-PQR=
S△PQR•h=
(
PQ•PRsinα)•PS•sinβ,记O到各面的距离为d,利用vS-PQR=vO-PQR+vO-PRS+vO-PQS,可得:PQ•PR•PS•sinβ=d(PQ•PR+PR•PS+PQ•PS),由此可得结论.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:解:设正三棱锥P-ABC中,各侧棱两两夹角为α,PC与面PAB所成角为β,
则vS-PQR=
S△PQR•h=
(
PQ•PRsinα)•PS•sinβ.
另一方面,记O到各面的距离为d,则vS-PQR=vO-PQR+vO-PRS+vO-PQS,
S△PQR•d=
△PRS•d+
S△PRS•d+
△PQS•d=
×
PQ•PRsinα+
×
PS•PRsinα+
×
PQ•PS•sinα,
故有:PQ•PR•PS•sinβ=d(PQ•PR+PR•PS+PQ•PS),
即
+
+
=
=常数.
故选D.
则vS-PQR=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
另一方面,记O到各面的距离为d,则vS-PQR=vO-PQR+vO-PRS+vO-PQS,
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| d |
| 3 |
| 1 |
| 2 |
| d |
| 3 |
| 1 |
| 2 |
| d |
| 3 |
| 1 |
| 2 |
故有:PQ•PR•PS•sinβ=d(PQ•PR+PR•PS+PQ•PS),
即
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| PS |
| sinβ |
| d |
故选D.
点评:本题考查三棱锥体积的计算,考查学生的探究能力,正确求体积是关键.

练习册系列答案
相关题目
设O是正三棱锥P-ABC底面是三角形ABC的中心,过O的动平面与PC交于S,与PA、PB的延长线分别交于Q、R,则和式
+
+
( )
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| PS |
| A、有最大值而无最小值 |
| B、有最小值而无最大值 |
| C、既有最大值又有最小值,两者不等 |
| D、是一个与面QPS无关的常数 |
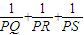 ( )
( )