题目内容
（f（x），g（x）g（x）≠0）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）＜f（x）g′（x），且f（-3）=0，
＜0的解集为（ ）
| f(x) |
| g(x) |
分析：令h（x）=
，利用f（x），g（x）（g（x）≠0）分别是定义在R上的奇函数和偶函数，即可判断出h（x）的奇偶性，再利用导数即可得出h（x）的单调性．
| f(x) |
| g(x) |
解答：解：令h（x）=
，∵f（x），g（x）（g（x）≠0）分别是定义在R上的奇函数和偶函数，
∴h（-x）=
=
=-h(x)，∴h（x）为R上的奇函数．
∵当x＜0时，f′（x）g（x）＜f（x）g′（x），∴h′(x)=
＜0，∴h（x）在（-∞，0）上单调递减，
又∵h（x）为R上的奇函数，∴h（x）在（0，+∞）上单调递减．
当x＜0时，由f（-3）=0，由h（x）单调递减可得
＜0的解集为{x|-3＜x＜0}；
当x＞0时，由f（-3）=-f（3）=0，由h（x）单调递减可得
＜0的解集为{x|3＜x}．
综上可知：
＜0的解集为{x|-3＜x＜0，或x＞3}．
故选C．
| f(x) |
| g(x) |
∴h（-x）=
| f(-x) |
| g(-x) |
| -f(x) |
| g(x) |
∵当x＜0时，f′（x）g（x）＜f（x）g′（x），∴h′(x)=
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
又∵h（x）为R上的奇函数，∴h（x）在（0，+∞）上单调递减．
当x＜0时，由f（-3）=0，由h（x）单调递减可得
| f(x) |
| g(x) |
当x＞0时，由f（-3）=-f（3）=0，由h（x）单调递减可得
| f(x) |
| g(x) |
综上可知：
| f(x) |
| g(x) |
故选C．
点评：熟练掌握函数的奇偶性、利用导数研究函数的单调性是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
；
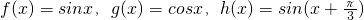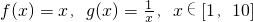的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．
；
的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．