题目内容
已知△ABC的内角A、B、C所对的边分别为a,b,c且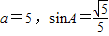 .
.(I) 若
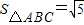 ,求周长的最小值;
,求周长的最小值;(Ⅱ) 若
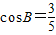 ,求边c的值.
,求边c的值.
【答案】分析:(I) 通过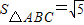 ,求出bc=10,写出周长利用基本不等式求出周长的最小值;
,求出bc=10,写出周长利用基本不等式求出周长的最小值;
(Ⅱ) 利用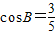 ,求出sinB,通过正弦定理与余弦定理求出边c的值.
,求出sinB,通过正弦定理与余弦定理求出边c的值.
解答:解:(I) 因为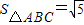 ,所以S=
,所以S= bcsinA=
bcsinA=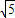 ,bc=10,
,bc=10,
∴l=b+c+5≥2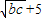 =2
=2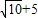 ,
,
当且仅当b=c=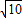 时,周长取最小值,
时,周长取最小值,
周长的最小值为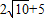 ;
;
(Ⅱ)∵cosB= >0,且0<B<π,∴sinB=
>0,且0<B<π,∴sinB=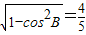 ,
,
由正弦定理得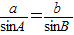 ,b=4
,b=4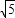 .
.
由余弦定理得:b2=a2+c2-2accosB,即80=c2+25-6c⇒c=11,或c=-2(舍去).
点评:本题考查三角形的边角关系,正弦定理与余弦定理的应用,基本不等式的应用,考查计算能力.
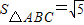 ,求出bc=10,写出周长利用基本不等式求出周长的最小值;
,求出bc=10,写出周长利用基本不等式求出周长的最小值;(Ⅱ) 利用
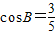 ,求出sinB,通过正弦定理与余弦定理求出边c的值.
,求出sinB,通过正弦定理与余弦定理求出边c的值.解答:解:(I) 因为
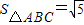 ,所以S=
,所以S= bcsinA=
bcsinA=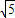 ,bc=10,
,bc=10,∴l=b+c+5≥2
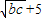 =2
=2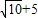 ,
,当且仅当b=c=
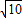 时,周长取最小值,
时,周长取最小值,周长的最小值为
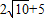 ;
;(Ⅱ)∵cosB=
 >0,且0<B<π,∴sinB=
>0,且0<B<π,∴sinB=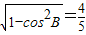 ,
,由正弦定理得
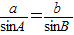 ,b=4
,b=4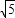 .
.由余弦定理得:b2=a2+c2-2accosB,即80=c2+25-6c⇒c=11,或c=-2(舍去).
点评:本题考查三角形的边角关系,正弦定理与余弦定理的应用,基本不等式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目