题目内容

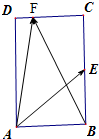
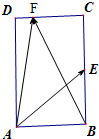如图在矩形ABCD中，AB=
3
，BC=4，点E为BC的中点，点F在CD上，若
AB
•
AF
=
3
，则
AE
•
BF
的值是（　　）
分析：由题意得选择基向量
AB
和
BC
，求出它们的长度和
AB
•
BC
=0，由向量加法的三角形法则求出
AF
，代入式子
AB
•
AF
=
3
由数量积运算求出|
DF
|，同理求出
AE
和
BF
，代入
AE
•
BF
进行化简求值．
解答：解：选基向量
AB
和
BC
，由题意得
AB
•
BC
=0，|
AB
|=
3
，|
BC
|=4，
∴
AF
=
AD
+
DF
=
BC
+
DF
，
∴
AB
•
AF
=
AB
•(
BC
+
DF
)=
AB
•
BC
+
AB
•
DF
=
3
，
即|
AB
||
DF
|cos0=
3
，解得|
DF
|=1，
∵点E为BC的中点，|
DF
|=1，
∴
AE
=
AB
+
1
2
BC
，
BF
=
BC
+
CF
=
BC
-
3
-1
3
AB
，
∴
AE
•
BF
=（
AB
+
1
2
BC
）•（
BC
-
3
-1
3
AB
）
=-
3
-1
3
AB
2+
1
2
BC
2=5+
3
，
故选B．
点评：本题考查了向量数量积的性质和运算律在几何中的应用，以及向量加法的三角形法则，关键是根据题意选基向量，其他向量都用基向量来表示．
练习册系列答案
相关题目
如图在矩形ABCD中，AB=2+
3
，BC=1，E为线段DC上一动点，现将△AED沿AE折起，使点D在面ABC上的射影K在直线AE上，当E从D运动到C，则K所形成轨迹的长度为（　　）
如图,在矩形ABCD中,AB=,BC=3,沿对角线BD将△BCD折起,使点C移至C′点,且C′在平面ABD上的射影恰好在AB上.

(1)求证:BC′⊥平面ADC′;

(2)求点A到平面BC′D的距离;

(3)设直线AB与平面BC′D所成的角为θ,求(用反正切表示).

如图在矩形ABCD中，AB=
3
，BC=4，点E为BC的中点，点F在CD上，若
AB
•
AF
=
3
，则
AE
•
BF
的值是（　　）
A．-5-
3
B．5+
3
C．4+
3
D．5-
3
精英家教网

如图在矩形ABCD中，AB=，BC=4，点E为BC的中点，点F在CD上，若，则的值是（　　）

　

A．

B．

C．

D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网