题目内容
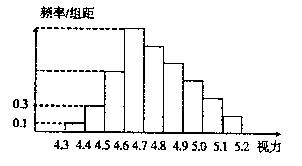
 随机抽查某中学高三年级100名学生的视力情况,得其频率分布直方图如图所示.已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为( )
随机抽查某中学高三年级100名学生的视力情况,得其频率分布直方图如图所示.已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为( )分析:先由频率分布直方图分析可得“视力在4.3~4.4的频数”对应的频率和“视力在4.4~4.5的频数”,再由等比数列的关系,得视力在4.6~4.7的频数,再根据样本容量是100,得出成等差数列后6组的频数的和,根据等差数列的前n项和公式进行求解即可.
解答:解:由频率分布直方图知,视力在4.3~4.4的频数为0.1×0.1×100=1,
视力在4.4~4.5的频数为0.3×0.1×100=3.因为前四组的频数成等比数列,
则视力在4.6~4.7的频数为1×33=27.
因为后6组的频数成等差数列,设公差为d,则6×27+
d=87,解得d=-5.
故视力在4.6~5.0之间的学生人数为4×27+
×(-5)=78(人).
故选A.
视力在4.4~4.5的频数为0.3×0.1×100=3.因为前四组的频数成等比数列,
则视力在4.6~4.7的频数为1×33=27.
因为后6组的频数成等差数列,设公差为d,则6×27+
| 6×5 |
| 2 |
故视力在4.6~5.0之间的学生人数为4×27+
| 6×5 |
| 2 |
故选A.
点评:本题主要考查阅读频率分布直方图的能力,以及等差数列与等比数列的综合运用,属于基础题.

练习册系列答案
相关题目